题目内容
如图,抛物线y=-x2+(m+2)x-3(m-1)交x轴于点A、B(A在B的右边),直线y=(m+1)x-3经过点A.若m<1.
(1)求抛物线和直线的解析式;
(2)直线y=kx(k<0)交直线y=(m+1)x-3于点P,交抛物线y=-x2+(m+2)x-3(m-1)于点M,过M点作x轴垂线,垂足为D,交直线y=(m+1)x-3于点N.问:△PMN能否为等腰三角形?若能,求k的值;若不能,请说明理由.

(1)求抛物线和直线的解析式;
(2)直线y=kx(k<0)交直线y=(m+1)x-3于点P,交抛物线y=-x2+(m+2)x-3(m-1)于点M,过M点作x轴垂线,垂足为D,交直线y=(m+1)x-3于点N.问:△PMN能否为等腰三角形?若能,求k的值;若不能,请说明理由.

(1)抛物线解析式为y=-x2+2x+3.直线解析式为y=x-3.
(2)如图,点C坐标为(0,-3),∠PNM=45°若△PNM为等腰三角形,且k<0,则PN=PM或PN=MN.
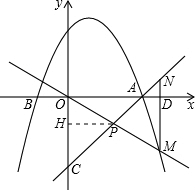
当PN=PM时,OD=DM,设M(m,-m),k=-1,
当PN=MN时,过点P作PH垂直y轴于点H.
PH=
OH=3-
点P坐标为(
,
-3)
则k=1-
.
综上所述,△PMN能为等腰三角形,k的值为-1或1-
.
(2)如图,点C坐标为(0,-3),∠PNM=45°若△PNM为等腰三角形,且k<0,则PN=PM或PN=MN.

当PN=PM时,OD=DM,设M(m,-m),k=-1,
当PN=MN时,过点P作PH垂直y轴于点H.
PH=
3
| ||
| 2 |
3
| ||
| 2 |
点P坐标为(
3
| ||
| 2 |
3
| ||
| 2 |
则k=1-
| 2 |
综上所述,△PMN能为等腰三角形,k的值为-1或1-
| 2 |

练习册系列答案
相关题目



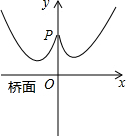 标系,左边的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称.
标系,左边的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称.