题目内容
已知抛物线y=ax2+bx+3交x轴于点A(x1,0)、B(-1,0)且x1>0,AO2+BO2=10,抛物线交y轴于点C,点D为抛物线的顶点.
(1)求抛物线的解析式;
(2)证明△ADC是直角三角形;
(3)第一象限内,在抛物线上是否存在一点E,使∠ECO=∠ACB?若存在,求出点E的坐标.

(1)求抛物线的解析式;
(2)证明△ADC是直角三角形;
(3)第一象限内,在抛物线上是否存在一点E,使∠ECO=∠ACB?若存在,求出点E的坐标.

(1)∵抛物线y=ax2+bx+3交x轴于点A(x1,0)、B(-1,0)
∴AO2+(-1)2=10,
∴AO2=9,
∴AO=±3,∴A(3,0)
把A(3,0)、B(-1,0)代入y=ax2+bx+3得:
解得:
,
∴抛物线的解析式:y=-x2+2x+3;
(2)证明:∵抛物线的解析式:
y=-x2+2x+3=-(x-1)2+4,
∴顶点D(1,4)
由(1)得:∴AC2=32+32=18,
CD2=2,AD2=20,
∴AD2=CD2+AC2,
∴△ADC是直角三角形.
(3)过A作AG⊥AC交CE于G,过G作GH⊥x轴于H,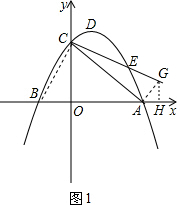
∵∠ECO=∠ACB,∴∠ECA=∠BCO,
∵∠COB=∠CAG,
∴Rt△BOC∽Rt△GAC,
∴
=
,
∴
=
,
∴AG=
由OC=OA,GH⊥x轴,
∴AH=GH,∴AH2+GH2=AG2
得AH=GH=1,
∴G点坐标为(4,1),
将C(0,3),G(4,1)代入y=kx+c得:
,
解得:
∴直线CG的解析式为:y=-
x+3,
联立:y=-
x+3与y=-x2+2x+3,
-
x+3=-x2+2x+3,
解得:x1=
,x2=0(与A点重合舍去),
x=
时,y=
,
∴E(
,
).
∴AO2+(-1)2=10,
∴AO2=9,
∴AO=±3,∴A(3,0)
把A(3,0)、B(-1,0)代入y=ax2+bx+3得:
|
解得:
|
∴抛物线的解析式:y=-x2+2x+3;
(2)证明:∵抛物线的解析式:
y=-x2+2x+3=-(x-1)2+4,
∴顶点D(1,4)
由(1)得:∴AC2=32+32=18,
CD2=2,AD2=20,
∴AD2=CD2+AC2,
∴△ADC是直角三角形.
(3)过A作AG⊥AC交CE于G,过G作GH⊥x轴于H,

∵∠ECO=∠ACB,∴∠ECA=∠BCO,
∵∠COB=∠CAG,
∴Rt△BOC∽Rt△GAC,
∴
| OB |
| AG |
| OC |
| AC |
∴
| 1 |
| AG |
| 3 | ||
3
|
∴AG=
| 2 |
由OC=OA,GH⊥x轴,
∴AH=GH,∴AH2+GH2=AG2
得AH=GH=1,
∴G点坐标为(4,1),
将C(0,3),G(4,1)代入y=kx+c得:
|
解得:
|
∴直线CG的解析式为:y=-
| 1 |
| 2 |
联立:y=-
| 1 |
| 2 |
-
| 1 |
| 2 |
解得:x1=
| 5 |
| 2 |
x=
| 5 |
| 2 |
| 7 |
| 4 |
∴E(
| 5 |
| 2 |
| 7 |
| 4 |

练习册系列答案
相关题目


 什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标.
什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标.
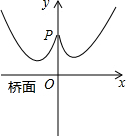 标系,左边的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称.
标系,左边的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称.