题目内容
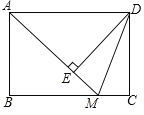
【题目】如图,在矩形ABCD中,M为BC上的点,过点D作DE⊥AM于E,DE=DC=5,AE=2EM.
(1)求证:BM=AE;
(2)求BM的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由矩形的性质推出∠DAE=∠AMB,AB=DE,∠ABC=∠AED=90°,求出△ADE≌△MAB,即可得BM=AE;
(2)根据勾股定理,将值代入求出EM即可求出BM.
(1)∵四边形ABCD是矩形,
∴AD∥BC,AB=CD,∠B=∠C=90°,
∴∠DAE=∠AMB
∵CD=DE,CD=AB,
∴AB=DE,且∠ABC=∠AED=90°,∠DAE=∠AMB,
∴△ADE≌△MAB,
∴BM=AE
(2)在Rt△ABM中,AM2=AB2+BM2,
∴9EM2=25+4EM2,
∴EM=![]() ,
,
∴AE=BM=2![]()

练习册系列答案
相关题目