题目内容
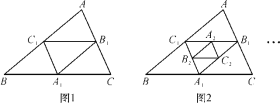
【题目】如图1,在正方形ABCD中,点E,F分别在AB,BC上,且AE=BF.
(1)试探索线段AF,DE的数量关系,写出你的结论并说明理由;
(2)连接EF,DF,分别取AE,EF,FD,DA的中点H,I,J,K,则四边形HIJK是什么特殊四边形?请在图2中补全图形,并说明理由.

【答案】(1)AF=DE.理由见解析;(2)见解析
【解析】试题分析:(1)根据已知利用SAS判定△DAE≌△ABF,由全等三角形的判定方法可得到AF=DE.
(2)根据已知可得HK,KJ,IJ,HI都是中位线,由全等三角形的判定可得到四边形四边都相等且有一个角是直角,从而来可得到该四边形是正方形.
试题解析:
(1)AF=DE.
理由:∵四边形ABCD是正方形,
∴AB=AD,∠DAB=∠ABC=90°.
又∵AE=BF,
∴△DAE≌△ABF(SAS).
∴AF=DE.
(2)如图所示:
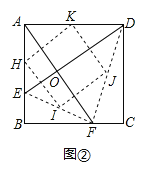
四边形HIJK是正方形.理由:
∵H,I,J,K分别是AE,EF,FD,DA的中点,
∴HI=KJ=![]() AF,HK=IJ=
AF,HK=IJ=![]() ED.
ED.
∵AF=DE,
∴HI=KJ=HK=IJ.
∴四边形HIJK是菱形.
∵△DAE≌△ABF,
∴∠ADE=∠BAF.
∵∠ADE+∠AED=90°,
∴∠BAF+∠AED=90°.
∴AF⊥DE.
∵HK∥DE,HI∥AF,
∴HK⊥HI.
∴∠KHI=90°.
∴四边形HIJK是正方形.

【题目】某商场计划购进甲、乙两种商品共![]() 件,这两种商品的进价、售价如表所示:
件,这两种商品的进价、售价如表所示:
进价(元/件) | 售价(元/件) | |
甲种商品 |
|
|
乙种商品 |
|
|
设购进甲种商品![]() (
(![]() ,且
,且![]() 为整数)件,售完此两种商品总利润为
为整数)件,售完此两种商品总利润为![]() 元.
元.
(1)该商场计划最多投入![]() 元用于购进这两种商品共
元用于购进这两种商品共![]() 件,求至少购进甲种商品多少件?
件,求至少购进甲种商品多少件?
(2)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)若售完这些商品,商场可获得的最大利润是__________元.