题目内容
【题目】如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°,则电视塔AB的高度为米(结果保留根号).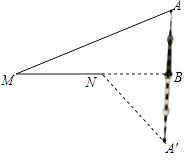
【答案】100 ![]()
【解析】如图,
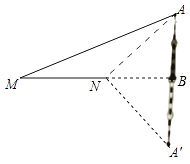
连接AN,由题意知,BM⊥AA',BA=BA'
∴AN=A'N,
∴∠ANB=∠A'NB=45°,
∵∠AMB=22.5°,
∴∠MAN=∠ANB﹣∠AMB=22.5°=∠AMN,
∴AN=MN=200米,
在Rt△ABN中,∠ANB=45°,
∴AB= ![]() AN=100
AN=100 ![]() (米),
(米),
故答案为100 ![]() .
.
构造直角三角形,利用三角函数的边角关系即可求出.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校学生会主席换届选举,经初选、复选后,共有甲,乙,丙三人进入最后的竞选,最后决定用投票方式进行选举,共发出1800张选票,得票数最高者为当选人,且废票不计入任何一位候选人的得票数内,全校设有四个投票箱,目前第一、第二、第三投票箱已开完所有选票,剩下第四投票箱尚未开票,结果如表所示:![]() 单位:票
单位:票![]()
投票箱 | 候选人 | 废票 | 合计 | ||
甲 | 乙 | 丙 | |||
一 | 200 | 211 | 147 | 12 | 570 |
二 | 244 | 15 | 630 | ||
三 | 97 | 41 | 205 | 7 | 350 |
四 | 250 | ||||
![]() 若第二投票箱候选人甲的得票数比乙的3倍还多31票,请分别求出第二投票箱甲、乙两名候选人的得票数.
若第二投票箱候选人甲的得票数比乙的3倍还多31票,请分别求出第二投票箱甲、乙两名候选人的得票数.
![]() 根据
根据![]() 题的数据分析,请判断乙侯选人是否还有机会当选,并详细解释或完整写出你的解题过程.
题的数据分析,请判断乙侯选人是否还有机会当选,并详细解释或完整写出你的解题过程.
【题目】为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系(一次函数)配套设计的,下表列出5套符合条件的课桌椅的高度. ①假设课桌的高度为ycm椅子的高度为xcm,请确定y与x的函数关系式;②现有一把高37cm的椅子和一张高71.5cm的课桌,它们是否配套?为什么?
椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |