题目内容
【题目】在平面直角坐标系中,A,B,C三点坐标分别为A(﹣6,3),B(﹣4,1),C(﹣1,1).
(1)如图1,顺次连接AB,BC,CA,得△ABC.
①点A关于x轴的对称点A1的坐标是 , 点B关于y轴的对称点B1的坐标是;
②画出△ABC关于原点对称的△A2B2C2;
③tan∠A2C2B2=;
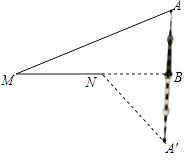
(2)利用四边形的不稳定性,将第二象限部分由小正方形组成的网格,变化为如图2所示的由小菱形组成的网格,每个小菱形的边长仍为1个单位长度,且较小内角为60°,原来的格点A,B,C分别对应新网格中的格点A′,B′,C′,顺次连接A′B′,B′C′,C′A′,得△A′B′C′,则tan∠A′C′B′= . 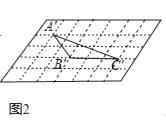
【答案】
(1)(﹣6,﹣3),(4,1),![]()
(2)![]()
【解析】(1)①点A关于x轴的对称点A1的坐标是(﹣6,﹣3),点B关于y轴的对称点B1的坐标是(4,1);
所以答案是:(﹣6,﹣3),(4,1);
②如图1所示; 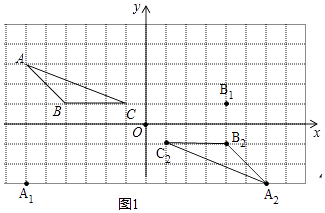
③tan∠A2B2C2= ![]() ;
;
所以答案是: ![]() ;
;
( 2 )如图2,过A'作A'E⊥B′C′于E,延长C′B′至D,使DC'=5,连接A'D,
Rt△A′ED中,∵∠A′DE=60°,A'D=2, 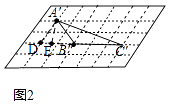
∴DE=1,A'E= ![]() ,
,
∴EC'=5﹣1=4,
Rt△A′EC′中,tan∠A'C'B'= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】本题主要考查了坐标与图形变化-对称和锐角三角函数的定义的相关知识点,需要掌握关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y);关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y);锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数才能正确解答此题.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案