题目内容
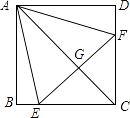
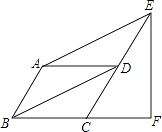
【题目】如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E. 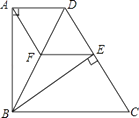
(1)求证:△ABD≌△EBD;
(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.
【答案】
(1)证明:如图,

∵AD∥BC,
∴∠1=∠DBC.
∵BC=DC,
∴∠2=∠DBC.
∴∠1=∠2.
∵BA⊥AD,BE⊥CD
∴∠BAD=∠BED=90°,
在△ABD和△EBD中  ,
,
∴△ABD≌△EBD(AAS)
(2)证明:由(1)得,AD=ED,∠1=∠2.
∵EF∥DA,
∴∠1=∠3.
∴∠2=∠3.
∴EF=ED.
∴EF=AD.
∴四边形AFED是平行四边形.
又∵AD=ED,
∴四边形AFED是菱形.
【解析】(1)首先证明∠1=∠2.再由BA⊥AD,BE⊥CD可得∠BAD=∠BED=90°,然后再加上公共边BD=BD可得△ABD≌△EBD;(2)首先证明四边形AFED是平行四边形,再有AD=ED,可得四边形AFED是菱形.
【考点精析】根据题目的已知条件,利用菱形的判定方法的相关知识可以得到问题的答案,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目