题目内容
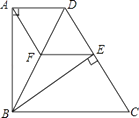
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连结AC交EF于G,下列结论:①BE=DF;②∠AEF=15°;③AC垂直平分EF;④BE+DF=EF;⑤△CEF为等腰直角三角形,其中正确的有(填序号). 
【答案】①③⑤
【解析】解:∵四边形ABCD是正方形,△AEF是等边三角形, ∴AB=AD,AE=AF,∠B=∠D,=90°,
在Rt△ABE和Rt△ADF中, ![]() ,
,
∴Rt△ABE≌Rt△ADF,
∴BE=DF,故①正确,
∵BC=DC,
∴CE=CF,
∴⑤△CEF为等腰直角三角形,
由于AE=AF,CW=CF,
∴AC垂直平分EF,故③⑤正确,
∵△AEF是等边三角形,∴∠AEF=60°,故②错误,
设EC=x,由勾股定理,得
EF= ![]() x,CG=
x,CG= ![]() x,
x,
AG=AEsin60°=EFsin60°=2×CGsin60°= ![]() x,
x,
∴AC= ![]() ,
,
∴AB= ![]() ,
,
∴BE= ![]() ﹣x=
﹣x= ![]() ,
,
∴BE+DF= ![]() x﹣x≠
x﹣x≠ ![]() x,故④错误,
x,故④错误,
所以答案是:①③⑤.
【考点精析】根据题目的已知条件,利用等腰直角三角形和线段垂直平分线的性质的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目