题目内容
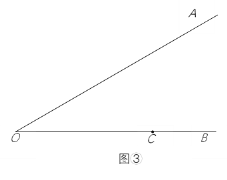
【题目】已知：如图，⊙O与⊙P相交于A、B两点，点P在⊙O上，⊙O的弦AC切⊙P于点A，CP及其延长线交⊙P于D、E，经过E作EF⊥CE交CB的延长线于F．
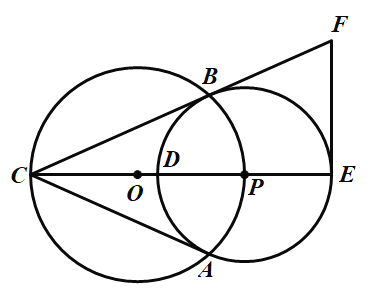
⑴求证：BC是⊙P的切线；
⑵若CD=2，CB=
，求EF的长；
⑶若设k=PE：CE，是否存在实数k，使△PBD恰好是等边三角形?若存在，求出k的值；若不存在，请说明理由．
【答案】（1）见解析；（2）
；（3）存在，
【解析】
（1）要证明BC是⊙P的切线，则连接BP，需要证明BP⊥BC．根据已知条件，连接AP．根据切线的性质得到∠PAC=90°，再根据圆周角定理的推论得到CP是直径，从而得到∠CBP=90°，证明结论；
（2）首先证得△BCD∽△ECB，求得CE的长，再根据Rt△EFC∽Rt△BPC求得EF的长；
（3）根据等边三角形的性质和含30度角的直角三角形的性质进行求解．
（1）连接PA、PB，
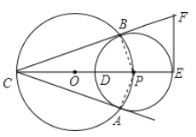
∵AC切⊙P于A，PA是⊙P的半径，
∴AC⊥PA．
即：∠PAC=90°，
∴CP是⊙O的直径，
∴∠PBC=90°，
即PB⊥CB，
又∵PB是⊙P的半径，
∴BC是⊙P的切线；
（2）连接BD、BE、PB，
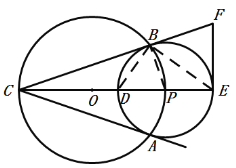
∵BC是⊙P的切线，
∴∠CBD=∠CEB，
又∠BCD=∠ECB，
∴△BCD∽△ECB，
∴
，
∵CD=2，CB=
，
∴CE=
，
DE=CE-CD=4-2=2．
∴PB=
DE =1，
在Rt△EFC和Rt△BPC中，∠ECF=∠BCP，∠FEC=∠PBC=90°，
∴Rt△EFC∽Rt△BPC，
∴
，
∴
；
（3）存在实数
时，△PBD为等边三角形．
理由如下：
∵△PBD为等边三角形，
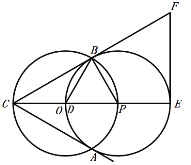
∴∠CPB=60°．
∵CB是⊙P的切线，
∴CB⊥BP，
∴∠BCP=30°，△PBC为直角三角形，
∴PB=PC，PB=PE，
∴PC=2PE，CE=PC+PE，
∴CE=3PE，
∴PE：CE=1：3，
即：时，△PBD为等边三角形．
【点晴】
本题考查了切线的判定和切线的性质以及相似三角形的判定和相似三角形的性质，勾股定理的应用，含30度角的直角三角形的性质．
