题目内容
【题目】类比探究:
(1)如图1,等边△ABC内有一点P,若AP=8,BP=15,CP=17,求∠APB的大小;(提示:将△ABP绕顶点A旋转到△ACP′处)
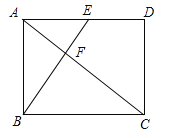
(2)如图2,在△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点,且∠EAF=45°.求证:EF2=BE2+FC2;
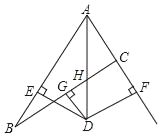
(3)如图3,在△ABC中,∠C=90°,∠ABC=30°,点O为△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,若AC=1,求OA+OB+OC的值.

【答案】(1)150°;(2)见解析;(3)![]() .
.
【解析】
(1)根据△APB绕着点A逆时针旋转60°得到△ACP′,根据旋转变换前后的两个三角形全等,全等三角形对应边相等,全等三角形对应角相等以及等边三角形的判定和勾股定理逆定理即可得到结论;
(2)把△ABE绕点A逆时针旋转90°得到△ACE′,根据旋转的性质可得AE′=AE,CE′=CE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,再求出∠E′AF=45°,从而得到∠EAF=∠E′AF,然后利用“边角边”证明△EAF和△E′AF全等,根据全等三角形对应边相等可得E′F=EF,再利用勾股定理列式即可得证;
(3)将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,根据直角三角形30°角所对的直角边等于斜边的一半求出AB=2AC,即A′B的长,再根据旋转的性质求出△BOO′是等边三角形,根据等边三角形的三条边都相等可得BO=OO′,等边三角形三个角都是60°求出∠BOO′=∠BO′O=60°,然后求出C、O、A′、O′四点共线,再利用勾股定理列式求出A′C,从而得到OA+OB+OC=A′C.
解:(1)如图1,将△APB绕着点A逆时针旋转60°得到△ACP′,
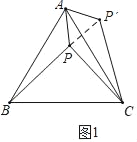
∴△ACP′≌△ABP,
∴AP′=AP=8、CP′=BP=15、∠AP′C=∠APB,
由题意知旋转角∠PA P′=60°,
∴△AP P′为等边三角形,
∴P P′=AP=8,∠A P′P=60°,
∵PP′2+P′C2=82+152=172=PC2,
∴∠PP′C=90°,
∴∠APB=∠AP′C=∠A P′P+∠P P′C=60°+90°=150°
(2)如图2,把△ABE绕着点A逆时针旋转90°得到△ACE′,
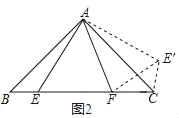
则AE′=AE,CE′=CE,∠CAE′=∠BAE,
∵∠BAC=90°,∠EAF=45°,
∴∠BAE+∠CAF=∠CAF+∠CAE′=∠FAE′=45°,
∴∠EAF=∠E′AF,且AE=AE',AF=AF,
∴△AEF≌△AE′F(SAS),
∴EF=E′F,
∵∠B+∠ACB=90°,
∴∠ACB+∠ACE′=90°,
∴∠FCE′=90°,
∴E′F2=CF2+CE′2,
∴EF2=BE2+CF2;
(3)如图3,将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,
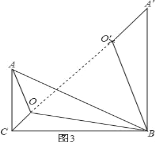
∵在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,
∴AB=2,
∴![]()
∵△AOB绕点B顺时针方向旋转60°,
∴△A′O′B如图所示;
∠A′BC=∠ABC+60°=30°+60°=90°,
∵∠ACB=90°,AC=1,∠ABC=30°,
∴AB=2AC=2,
∵△AOB绕点B顺时针方向旋转60°,得到△A′O′B,
∴A′B=AB=2,BO=BO′,A′O′=AO,
∴△BOO′是等边三角形,
∴BO=OO′,∠BOO′=∠BO′O=60°,
∵∠AOC=∠COB=∠BOA=120°,
∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°,
∴C、O、A′、O′四点共线,
在Rt△A′BC中,![]() ,
,
∴OA+OB+OC=A′O′+OO′+OC=A′C=![]() .
.

【题目】某冷库一天的冷冻食品进出记录如下表![]() 运进用正数表示,运出用负数表示
运进用正数表示,运出用负数表示![]() :
:
进出数量 |
| 4 |
| 2 |
|
进出次数 | 2 | 1 | 3 | 3 | 2 |
(1)这天冷库的冷冻食品比原来增加了还是减少了?请说明理由.
(2)根据实际情况,现有两种方案:
方案一:运进每吨冷冻食品费用500元,运出每吨冷冻食品费用800元.
方案二:不管运进还是运出每吨冷冻食品费用都是600元.从节约运费的角度考虑,选用哪一种方案比较合适?