题目内容
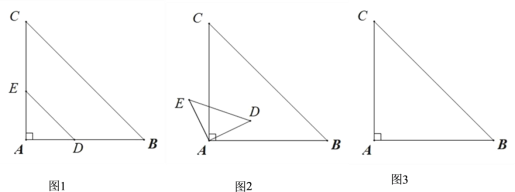
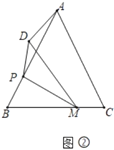
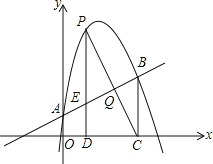
【题目】如图,抛物线y=ax2+bx+1经过点(2,6),且与直线y=![]() x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
【答案】(1)y=-x2+![]() x+1;(2)当x=2时,PE的最大值为4;(3)点Q的坐标为(
x+1;(2)当x=2时,PE的最大值为4;(3)点Q的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)利用直线解析式可求得B点坐标,再利用待定系数法可求得抛物线解析式;
(2)设出P点坐标,则可表示出E点坐标,则可表示出PE的长,利用二次函数的性质可求得PE的最大值;
(3)由条件可知四边形BCEP为平行四边形,可得BC=PE,则可求得P点坐标,利用中点坐标可求得Q点坐标.
(1)∵BC⊥x轴,垂足为点C(4,0),且点B在直线y=![]() x+1上,
x+1上,
∴点B的坐标为(4,3),
∴抛物线y=ax2+bx+1经过点(2,6)和点B(4,3),
∴![]() ,解得
,解得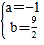 ,
,
∴抛物线的解析式为y=-x2+![]() x+1;
x+1;
(2)设动点P的坐标为(x,-x2+![]() x+1),则点E的坐标为:(x,
x+1),则点E的坐标为:(x,![]() x+1),
x+1),
∵PD⊥x轴于点D,且点P在x轴上,
∴PE=PD-ED=-x2+![]() x+1-(
x+1-(![]() x+1)=-x2+4x=-(x-2)2+4,
x+1)=-x2+4x=-(x-2)2+4,
∴当x=2时,PE的最大值为4;
(3)∵PC与BE互相平分,
∴四边形BCEP为平行四边形,
∴PE=BC,
∴-x2+4x=3即x2-4x+3=0,解得x1=1,x2=3,
∵点Q分别是PC,BE的中点,且点Q在直线y=![]() x+1
x+1
∴①当x=1时,点Q的横坐标为![]() ,点Q的坐标为(
,点Q的坐标为(![]() ,
,![]() ),
),
②当x=3时,点Q的横坐标为![]() ,点Q的坐标为(
,点Q的坐标为(![]() ,
,![]() ),
),
综上可知点Q的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】某服装商城每月付给销售人员的工资有两种方案,已知计件工资与销售件数成正比例.有甲、乙两种品牌服装销售人员,如果销售量为![]() 件,销售甲品牌服装的工资是
件,销售甲品牌服装的工资是![]() (元),销售乙品牌服装的工资是
(元),销售乙品牌服装的工资是![]() (元),销售件数与工资之间的关系如图所示,已知销售甲品牌服装的每月底薪是800元,每销售一件甲品牌服装每件所得的提成比乙高2元,不管销售那种品牌服装,销售量超过80件(不含80件),
(元),销售件数与工资之间的关系如图所示,已知销售甲品牌服装的每月底薪是800元,每销售一件甲品牌服装每件所得的提成比乙高2元,不管销售那种品牌服装,销售量超过80件(不含80件),
则每件多提成6元.下表是半年内甲乙两产品的销售量:
时间 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
甲品牌服装销量 | 90 | 120 | 130 | 80 | 100 | 110 |
乙品牌服装销量 | 70 | 60 | 90 | 80 | 110 | 100 |
(1)现从半年内随机抽取1个月,求这一月乙品牌服装销售量超过80件(不含80)的概率;
(2)根据图中信息,求销售乙品牌服装的底薪是多少元?
(3)小明拟销售甲、乙两种品牌服装,如果仅从工资收人的角度考虑,请利用所学的统计知识帮他选择,并说明理由.