Question

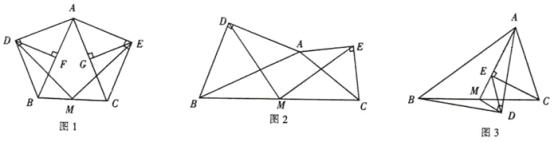
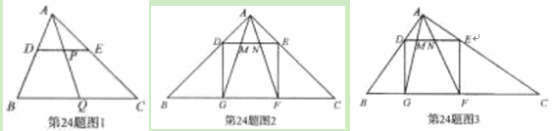
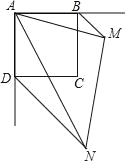
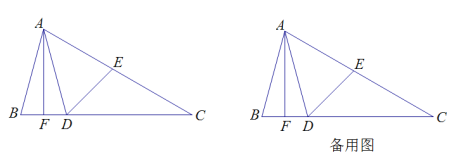
【题目】如图，在△ABC中，CA＝CB，AB＝10，0°＜∠C＜60°，AF⊥BC于点F，在FC上截取FD＝FB，点E是AC上一点，连接DA、DE，且∠ADE＝∠B.

（1）求证：ED＝EC；

（2）若∠C＝30°，求BD长；

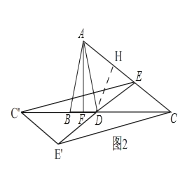
（3）在（2）的条件下，将图中△DEC绕点D逆时针旋转得到△DE′C′，请问在旋转的过程中，以点C、E、C′、E′为顶点的四边形可以构成平行四边形吗？若可以，请求出该平行四边形的面积，若不可以，请说明理由.

Answer 1

【答案】（1）见解析；（2）BD=10；（3）可以，见解析，.

【解析】

（1）先判断出∠C=180°-2∠ABC，∠CDE=180°-2∠ABC，进而求出∠C=∠CDE，即可得出结论；（2）先求出角BAD=30°，进而求出BG，AG，即可得出DG，最后用勾股定理即可得出结论；（3）先判断出旋转到C落在CB的延长线上，以点C,E,C’,E’为顶点的四边形是平行四边形，再求出DH，DE即可得出结论.

解：（1）∵AC=BC,

∴∠ABC=∠BAC，

∴∠C=180°-∠ABC-∠BAC=180°-2∠ABC，

∵AF⊥BC，BF=DF,

∴AB=AD，

∴∠ADB=∠ABC，

∴∠CDE=180°-∠ADE-∠ADB=180°-2∠ABC

∴∠CDE=∠C，

∴ED=CE；

（2）∵∠C=30°，

∴∠ABC=∠ADB=∠BAC=∠ADE=75°，

∴∠BAD=30°，

过点B作BG⊥AD于G，如图1，

在Rt△ABG中，AB=10，∠BAD=30°，

∴BG=5，AG=5

∴DG=AD-AG=10-5=5(2-)

在Rt△BDG中，BD=

（3）存在，理由：

如图2，当点C’落在CB延长线上，点E’落在ED的延长线上，

由旋转知DE=DE’,DC=DC’

∴四边形CEC’E’是平行四边形，

过点D作DH⊥AC于H，

在Rt△ADH中，AD=10，∠DAH=∠BAC-∠BAD=45°，

∴DH=5

在Rt△DEH中，∠AED=∠ACB+∠CDE=60°，

∴∠EDH=30°，

∴DE=

∴CE=

∴S平行四边形CEC’E’=4S△CDE=