题目内容
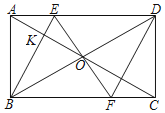
【题目】如图,在ABCD中,对角线AC,BD相交于点O,过点O作BD的垂线与边AD,BC分别交于点E,F,连接BE交AC于点K,连接DF.
(1)求证:四边形EBFD是菱形;
(2)若BK=3EK,AE=4,求四边形EBFD的周长.
【答案】![]() 见解析;
见解析;![]() 32
32
【解析】
(1)四边形ABCD是平行四边形,可以证明△DEO≌△BFO,可得OE=OF,从而四边形EBFD是平行四边形,根据EF⊥BD,进而可得平行四边形EBFD是菱形;
(2)证明△AEK∽△CBK,对应边成比例可得BC=12,进而求出DE的长,可得菱形的周长.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EDO=∠FBO,
OB=OD,
∠EOF=∠FOB,
∴△DEO≌△BFO(ASA),
∴OE=OF,
∴四边形EBFD是平行四边形,
∵EF⊥BD,
∴平行四边形EBFD是菱形;
(2)∵AE∥BC,
∴△AEK∽△CBK,
∴![]() ,
,
∵BK=3EK,AE=4,
∴![]() ,
,
∴BC=12,
∴AD=BC=DE+AE=DE+4=12
∴DE=8,
∴菱形EBFD的周长为4DE=32.
答:四边形EBFD的周长为32.

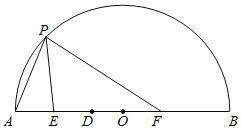
【题目】如图,D是直径AB上一定点,E,F分别是AD,BD的中点,P是![]() 上一动点,连接PA,PE,PF.已知AB=6cm,设A,P两点间的距离为xcm,P,E两点间的距离为y1cm,P,F两点间的距离为y2cm.
上一动点,连接PA,PE,PF.已知AB=6cm,设A,P两点间的距离为xcm,P,E两点间的距离为y1cm,P,F两点间的距离为y2cm.
小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0.97 | 1.27 |
| 2.66 | 3.43 | 4.22 | 5.02 |
y2/cm | 3.97 | 3.93 | 3.80 | 3.58 | 3.25 | 2.76 | 2.02 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
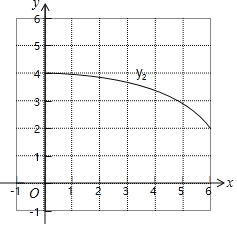
(3)结合函数图象,解决问题:当△PEF为等腰三角形时,AP的长度约为 cm.
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) | x60 | x |
售价(元/件) | 200 | 100 |
若用1800元购进甲种商品的件数与用900元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共100件,其中销售甲种商品为a件(a40),设销售完100件甲、乙两种商品的总利润为w元,求w与a之间的函数关系式,并求出w的最小值.
【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别 | 身高 |
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组;
(2)样本中,女生身高在E组的人数有 人;
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?

【题目】弹簧原长(不挂重物)15cm,弹簧总长L(cm)与重物质量x(kg)的关系如下表所示:
弹簧总长L(cm) | 16 | 17 | 18 | 19 | 20 |
重物重量x(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
当重物质量为5kg(在弹性限度内)时,弹簧总长L(cm)是( )
A.22.5B.25C.27.5D.30
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的