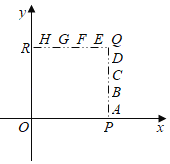��Ŀ����
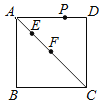
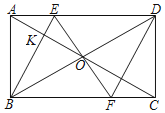
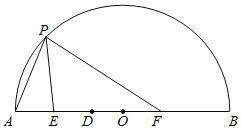
����Ŀ����ͼ��D��ֱ��AB��һ���㣬E��F�ֱ���AD��BD���е㣬P��![]() ��һ���㣬����PA��PE��PF����֪AB��6cm����A��P�����ľ���Ϊxcm��P��E�����ľ���Ϊy1cm��P��F�����ľ���Ϊy2cm��
��һ���㣬����PA��PE��PF����֪AB��6cm����A��P�����ľ���Ϊxcm��P��E�����ľ���Ϊy1cm��P��F�����ľ���Ϊy2cm��
С�ڸ���ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
������С�ڵ�̽�����̣��벹��������
��1�������±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���y1��y2��x�ļ����Ӧֵ��
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0.97 | 1.27 | �� �� | 2.66 | 3.43 | 4.22 | 5.02 |
y2/cm | 3.97 | 3.93 | 3.80 | 3.58 | 3.25 | 2.76 | 2.02 |
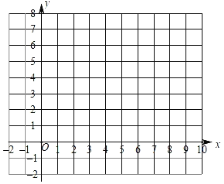
��2����ͬһƽ��ֱ������ϵxOy�У������ȫ��ı��и�����ֵ����Ӧ�ĵ㣨x��y1������x��y2��������������y1��y2��ͼ��
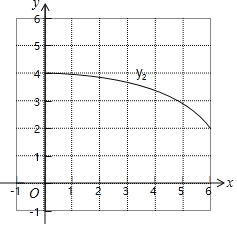
��3����Ϻ���ͼ������⣺����PEFΪ����������ʱ��AP�ij���ԼΪ�� ��cm��
���𰸡���1��1.90����2������������3��3.5��3.8��4.8
��������
��1��ͨ����ͼ�������ɵñ��е�������ֵ��
��2���ѱ���������赽ƽ��ֱ������ϵ�У�����ƽ�����������Ӽ��ɻ�������y1��y2��ͼ��
��3����Ϻ���ͼ���ɵõ���PEFΪ����������ʱ��AP�ij��ȣ�
��1��ͨ��������֪��
���е�������ֵ��1.90��
�ʴ�Ϊ��1.90��
��2������y1��y2��ͼ����ͼ��

��3���۲�ͼ���֪��
��PEFΪ���������Σ��ٵ�PE=PFʱ��![]() ���������Ľ��㣬AP�ij���ԼΪ3.8 cm���ڵ�PE=EFʱ��
���������Ľ��㣬AP�ij���ԼΪ3.8 cm���ڵ�PE=EFʱ��![]() ��AP�ij���ԼΪ3.5cm���۵�PF=EFʱ��
��AP�ij���ԼΪ3.5cm���۵�PF=EFʱ��![]() ��AP�ij���ԼΪ4.8 cm��
��AP�ij���ԼΪ4.8 cm��
�ʴ�Ϊ��3.5��3.8��4.8��

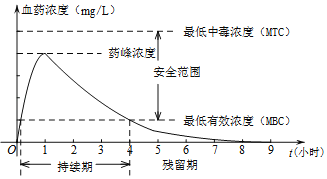
����Ŀ�������ٹ����¿�������״�����Ķ���������õ�����Ч���ƣ����ڸ�����ҵ��2��9�պ���븴��״̬��Ϊ���˽�ȫ����ҵ����ĸ�����������Dz����˽�ֹ��2020��3��1��ȫ������ʡ�ݵĸ����ʣ��������ݽ��������������ͷ��������������һЩ��Ϣ��

a����ֹ3��1��20ʱ��ȫ������11��ʡ�ݹ�ҵ��ҵ��������90%���ϣ���Ҫλ�ڶ����غ�������λ��ǰ���ķֱ��ǹ��ݣ�100%�����㽭��99.8%�������գ�99%����
b����ʡ�ݸ��������ݵ�Ƶ���ֲ�ֱ��ͼ��ͼ1�����ݷֳ�6�飬�ֱ���40��x��50��
50��x��60��60��x��70��70��x��80��80��x��90��90��x��100����
c����ͼ2����b�Ļ����ϣ���������ͳ��ͼ��
d����ֹ��2020��3��1�ո�ʡ�ݵĸ�������80��x��90��һ��������ǣ�
81.3 | 83.9 | 84 | 87.6 | 89.4 | 90 | 90 |
e����ֹ��2020��3��1�ո�ʡ�ݵĸ����ʵ�ƽ��������λ�����������£�
���� | ƽ���� | ��λ�� | ���� |
��ֹ��2020��3��1�� | 80.79 | m | 50��90 |
�����������⣺
��1���������⣬��ȫƵ���ֲ�ֱ��ͼ��
��2������ͳ��ͼ��50��x��60�����Բ�ĽǶ������� ���ȣ���ȷ��0.1����
��3����λ��m��ֵ���� ����
��4����������ͳ��ͼ������������ҵ��ֹ3��1�յĸ����ʷֲ�������