题目内容
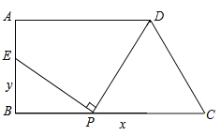
【题目】如图：梯形ABCD中，AD∥BC，∠ABC=90°，AD=9，BC=12，AB=6，在线段BC上任取一点P，连接DP，作射线PE⊥DP，PE与直线AB交于点E.
（1）试确定当CP=3时，点E的位置；
（2）若设CP=x，BE=y，试写出y关于自变量x的函数关系式.
【答案】（1）点E与点B重合；（2）当点P在BF上：
；当点P在CF上：
【解析】
（1）当CP=3时，易知四边形ADPB是矩形，由DP⊥BC，PE⊥DP，得出点E与点B重合；
（2）作DF⊥BC，F为垂足．欲求y关于自变量x的函数关系式，分为两种情况点P在BF上，点P在CF上，通过证明△PEB∽△DPF分别得出．
解：（1）连接DP
∵CP=3
∴BP=BC—CP=12—3=9
∵AD=9
∴AD=DP
∵AD∥DP，∠ABC=90°，
∴∠A=90°，
∴四边形ABPD是矩形
∴ DP⊥BP
∵PE⊥DP
∴点E与点B重合
（2）过点D作DF⊥BC，垂足为F，
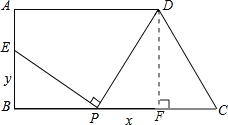
∴AD=BF=9 ，AB=DF=6
当点P在BF上：
∵∠BPE +∠EPD+∠DPF=180°，PE⊥PD，
∴∠BPE +∠DPF=90°，
∵DF⊥BC，
∴∠PDF+∠DPF=90°，
∴∠PDF =∠EPB，
∴△PEB∽△DPF，
∴
，
∵CP=x，BE=y ，
∴BP=12—x PF=PC—CF=x—3，
∴
，
∴
，
当点P在CF上，同理可求得：
．
练习册系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
