Question

【题目】如图，二次函数y＝2mx2+5mx﹣12m（m为参数，且m＜0）的图象与x轴交于点A、B，与y轴交于点C，点A的坐标为（﹣4，0）．

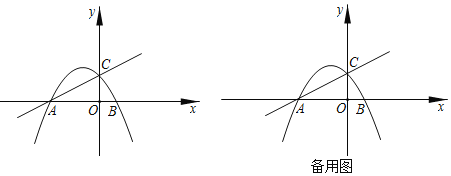
（1）求直线AC的解析式（用含m的式子表示）．

（2）若m＝﹣，连接BC，判断∠CAB和∠CBA的数量关系，并说明理由．

（3）在（2）的条件下，设点M为AC上方的抛物线上一动点（与点A，C不重合），以M为圆心的圆与直线AC相切，求⊙M面积的取值范围．

Answer 1

【答案】（1）y＝﹣3mx﹣12m；（2）∠CBA＝2∠CAB；（3）0＜S⊙M≤．

【解析】

（1）由抛物线的解析式求出C点坐标，再用待定系数法求直线AC的解析式；

（2）作点B关于y轴的对称点B'，连接CB'．证明AB'＝CB'便可得结论；

（3）过M点ME∥y轴，交AC于点E，设M点的横坐标为m，用m表示MD，再根据二次函数的性质求得MD的最大值，最后根据圆的面积公式便可求得结果．

（1）令x＝0，得y＝2mx2+5mx﹣12m＝﹣12m，

设直线AC的解析式为y＝kx+b（k≠0），则，

∴，

∴直线AC的解析式为：y＝﹣3mx﹣12m；

（2）∠CBA＝2∠CAB．

理由如下：

如图1，作点B关于y轴的对称点B'，连接CB'．

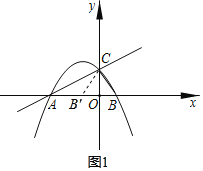
∴CB＝CB'，

∴∠CBA＝∠CB'O，

∵m＝﹣时，抛物线的解析式为：，

∴C（0，2），

∴OC＝2，

当y＝0，得＝0，

解得x＝﹣4或，

∴A（﹣4，0），B（，0），

∴B'（﹣，0），

∴AB'＝，CB'＝

∴AB'＝CB'，

∴∠CAB＝∠ACB'，

∵∠CB'O＝∠CAB+∠ACB'＝2∠CAB，

∴∠CBA＝2∠CAB；

（3）如图2，以MD为半径做圆，过M点ME∥y轴，交AC于点E，

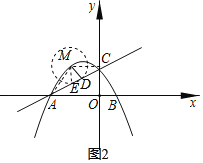
则∠MEC＝∠ACO，

∵A（﹣4，0），以（0，2）

∴直线AC的解析式为y＝，

设M（m，）（﹣4＜m＜0），则E（m，），

∴，

在Rt△AOC中，OC＝2，OA＝4，由勾股定理可得AC＝2，

∴sin∠MED＝，

∴，

由二次函数的性质知，当m＝﹣2时，DE有最大值为：，

∴，

∴⊙M面积的最大值为：π×（）2＝，

∴⊙M面积的取值范围为：0＜S⊙M≤．