题目内容
【题目】将抛物线![]() 向右平移2个单位,得到抛物线
向右平移2个单位,得到抛物线![]() 的图象
的图象![]() 是抛物线
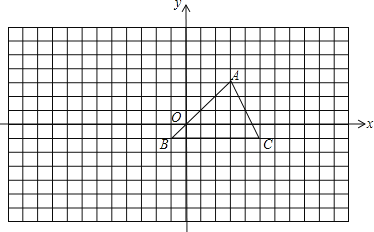
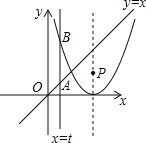
是抛物线![]() 对称轴上的一个动点,直线
对称轴上的一个动点,直线![]() 平行于y轴,分别与直线
平行于y轴,分别与直线![]() 、抛物线
、抛物线![]() 交于点A、
交于点A、![]() 若
若![]() 是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则
是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则![]() ______ .
______ .
【答案】![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
根据函数图象的平移规律,将![]() 向右平移2个单位,横坐标减2表示出抛物线
向右平移2个单位,横坐标减2表示出抛物线![]() 的函数解析式.然后再根据题目条件表示出点A、B的坐标,进而能够表示出AB的长度与AP的长度,然后根据等腰直角三角形的两直角边相等列出方程求解即可.
的函数解析式.然后再根据题目条件表示出点A、B的坐标,进而能够表示出AB的长度与AP的长度,然后根据等腰直角三角形的两直角边相等列出方程求解即可.
解:![]() 抛物线
抛物线![]() 向右平移2个单位,
向右平移2个单位,
![]() 抛物线
抛物线![]() 的函数解析式为
的函数解析式为![]() ,
,
![]() 抛物线
抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,
,
![]() 直线
直线![]() 与直线
与直线![]() 、抛物线
、抛物线![]() 交于点A、B,
交于点A、B,
![]() 点A的坐标为
点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,
,
![]() ,
,
![]() ,
,
![]() 是以点A或B为直角顶点的三角形,
是以点A或B为直角顶点的三角形,
![]() ,
,
![]() 或
或![]() ,
,
整理![]() 得,
得,![]() ,
,
解得![]() ,
,![]() ,
,
整理![]() 得,
得,![]() ,
,
解得![]() ,
,![]() ,
,
综上所述,满足条件的t值为:![]() 或
或![]() 或
或![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目