Question

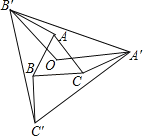
【题目】如图，O是边长为1的等边△ABC的中心，将AB、BC、CA分别绕点A、点B、点C顺时针旋转α（0°＜α＜180°），得到AB′、BC′、CA′，连接A′B′、B′C′、A′C′、OA′、OB′．（1）∠A′OB′＝___°；（2）当α＝___°时，△A′B′C′的周长最大．

Answer 1

【答案】（1）120； （2）150．

【解析】

（1）△A'B'C'是等边三角形，根据中心角的定义求解；

（2）当O，A，B'三点在一条直线上时，B'在OA的延长线上时，OB'最大，A′B′C′边长最大，则△A′B′C′的周长最大．

（1）∠A′OB′＝＝120°，

故答案是：120；

（2）△A'B'C'是等边三角形，△A′B′C′的周长最大，则边长最大，则OB'最大，当O，A，B'三点在一条直线上时，B'在OA的延长线上，OB'最大．

∠BAO＝∠BAC＝30°，

则a＝180°﹣30°＝150°．

故答案是：150．