题目内容
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,直线
点,直线![]() 交抛物线于点
交抛物线于点![]() ,并且,
,并且,![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)已知点![]() 为抛物线上一动点,且在第二象限,顺次连接点
为抛物线上一动点,且在第二象限,顺次连接点![]() 、
、![]() 、
、![]() 、
、![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
(3)在(2)中四边形![]() 面积最大的条件下,过点
面积最大的条件下,过点![]() 作直线平行于
作直线平行于![]() 轴,在这条直线上是否存在一个以
轴,在这条直线上是否存在一个以![]() 点为圆心,
点为圆心,![]() 为半径且与直线
为半径且与直线![]() 相切的圆?若存在,求出圆心
相切的圆?若存在,求出圆心![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
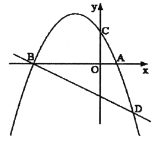
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 四边形
四边形![]() 取得最大值,最大值为9;(3)存在,点Q 为
取得最大值,最大值为9;(3)存在,点Q 为![]() 或
或![]() .
.
【解析】
(1)过点D作DE⊥x轴,垂足为E,由点D的坐标结合tan∠DBA=![]() ,可求出点B的坐标,根据点B,D的坐标,利用待定系数法即可求出抛物线的解析式;
,可求出点B的坐标,根据点B,D的坐标,利用待定系数法即可求出抛物线的解析式;
(2)过点M作MF⊥x轴,垂足为F,利用二次函数图象上点的坐标特征可求出A,C的坐标,设点M的坐标为(m,![]() )(-4<m<0),则点F的坐标为(m,0),由S四边形BMCA=S△BMF+S梯形FMCO+S△OCA可得出S四边形BMCA关于m的函数关系式,再利用二次函数的性质即可求出四边形BMCA面积的最大值;
)(-4<m<0),则点F的坐标为(m,0),由S四边形BMCA=S△BMF+S梯形FMCO+S△OCA可得出S四边形BMCA关于m的函数关系式,再利用二次函数的性质即可求出四边形BMCA面积的最大值;
(3)连接BC,易证△BOC∽△COA,进而可得出BC⊥AC,由点A,B,C的坐标,利用待定系数法可求出直线BC,AC的解析式,设点Q的坐标为(-2,n),由平行线的性质可得出过点Q且垂直AC的直线的解析式为y=![]() x+n+1,联立该直线与AC的解析式成方程组,通过解方程组可求出交点的坐标,再由该点到点Q的距离等于线段OQ的长度可得出关于n的一元二次方程,解之即可得出结论.
x+n+1,联立该直线与AC的解析式成方程组,通过解方程组可求出交点的坐标,再由该点到点Q的距离等于线段OQ的长度可得出关于n的一元二次方程,解之即可得出结论.
解:(1)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,如图1所示,
,如图1所示,
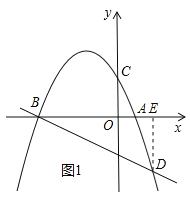
∵点![]() 的坐标为
的坐标为![]()
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
将![]() ,
,![]() 代入
代入![]() ,得:
,得:
![]() ,解得:
,解得: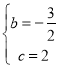 ,
,
∴抛物线的解析式为![]() .
.
(2)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,如图2所示,
,如图2所示,
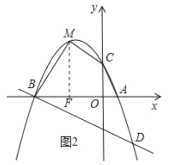
当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
当![]() 时,
时,![]() ,
,
∴点![]() 的坐标为(0,2).
的坐标为(0,2).
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() 四边形
四边形![]() 梯形
梯形![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() .
.
∵![]() ,
,
∴当![]() 时,
时,![]() 四边形
四边形![]() 取得最大值,最大值为9.
取得最大值,最大值为9.
(3)连接![]() ,如图3所示,
,如图3所示,
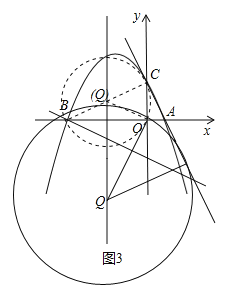
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为(0,2),点
的坐标为(0,2),点![]() 的坐标为(1,0),
的坐标为(1,0),
∴直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() (可利用待定系数法求出).
(可利用待定系数法求出).
设点![]() 的坐标为
的坐标为![]() ,则过点
,则过点![]() 且垂直
且垂直![]() 的直线的解析式为:
的直线的解析式为:![]() .
.
联立两直线解析式成方程组,得:
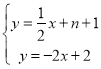 ,解得:
,解得: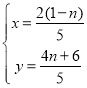 ,
,
∴两直线的交点坐标为![]() .
.
依题意,得: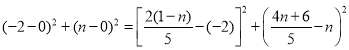
整理,得![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
综上所述:在这条直线上存在一个以![]() 点为圆心,
点为圆心,![]() 为半径且与直线
为半径且与直线![]() 相切的圆,点
相切的圆,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

【题目】为了增强学生对新冠病毒预防知识的了解,我校初一年级开展了网上预防知识的宣传教育活动.为了解这次宣传教育活动的效果,学校从初一年级1500名学生中随机抽取部分学生进行网上知识测试(测试满分100分,得分均为整数),并根据抽取的学生测试成绩,制作了如下统计图表:
抽取学生知识测试成绩的频数表 | ||
成绩 | 频数(人) | 频率 |
| 10 | 0.1 |
| 15 |
|
|
| 0.2 |
| 40 |
|
|
|
|
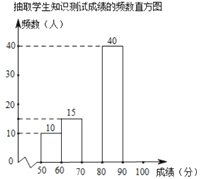
由图表中给出的信息回答下列问题:
(1)![]() ,
,![]() ,并补全频数直方图;
,并补全频数直方图;
(2)如果80分以上(包括80分)为优秀,请估计初一年级1500名学生中成绩优秀的人数;
(3)小强在这次测试中成绩为85分,你认为85分一定是这100名学生知识测试成绩的中位数吗?请简要说明理由.