题目内容
【题目】动手操作:
(1)如图1,将一块直角三角板DEF放置在直角三角板ABC上,使三角板DEF的两条直角边DE、DF分别经过点B、C,且BC∥EF,已知∠A=30°,则∠ABD+∠ACD= 度;
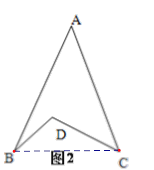
(2)如图2,∠BDC与∠A、∠B、∠C之间存在着什么关系,并说明理由;
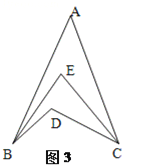
(3)灵活应用:请你直接利用以上结论,解决以下列问题:如图3,BE平分∠ABD,CE平分∠ACD,若∠BAC=40°,∠BDC=120°,求∠BEC的度数。



【答案】(1)60°;(2)猜想:∠A+∠B+∠C=∠BDC ,证明见解析;(3)∠BEC=80°;
【解析】试题分析:(1)在△BDC中,由三角形内角和定理可得∠DBC+∠DCB=90°,再由∠ABC+∠ACB=150°,从而可得;
(2)连接BC,利用三角形内角和定理推导即可得;
(3)由(2)可知∠A+∠ABD+∠ACD=∠BDC,∠A+∠ABE+∠ACE=∠BEC,再根据角平分线的定义即可得.
试题解析:(1)60°;
(2)猜想:∠A+∠B+∠C=∠BDC ;
证明如下:连接BC,
在△DBC中,∵∠DBC+∠DCB+∠D=180°,
∴∠DBC+∠DCB=180°﹣∠BDC;
在Rt△ABC中,
∵∠ABC+∠ACB+∠A=180°,
即∠ABD+∠DBC+∠DCB+∠ACD+∠A=180°,
而∠DBC+∠DCB=180°﹣∠BDC,
∴∠A+∠ABD+∠ACD=180°﹣(180°﹣∠BDC)=∠BDC,
即:∠A+∠B+∠C=∠BDC.
(3)灵活应用:
由(2)可知∠A+∠ABD+∠ACD=∠BDC,∠A+∠ABE+∠ACE=∠BEC,
∵∠BAC=40°,∠BDC=120°,
∴∠ABD+∠ACD=120°﹣40°=80°
∵BE平分∠ABD,CE平分∠ACB,
∴∠ABE+∠ACE=40°,
∴∠BEC=40°+40°=80°;