题目内容
【题目】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E.试猜想CE与BD的数量关系,并说明理由.

【答案】CE=![]() BD
BD
【解析】试题分析:
结合图形和已知条件直观感觉CE=![]() BD,但在原图中确难以证明,说明这道题需要作辅助线.考虑到把角的一边沿角平分线折叠后,会与另一边重合,即若把BC沿BD折叠,则点C会落到BA的延长线上,设这个落点为F,则CE=
BD,但在原图中确难以证明,说明这道题需要作辅助线.考虑到把角的一边沿角平分线折叠后,会与另一边重合,即若把BC沿BD折叠,则点C会落到BA的延长线上,设这个落点为F,则CE=![]() CF,(如下图),而此时我们再来观察,就发现很容易证得△BAD≌△CAF,从而可得CF=BD,进一步就可得CE=
CF,(如下图),而此时我们再来观察,就发现很容易证得△BAD≌△CAF,从而可得CF=BD,进一步就可得CE=![]() BD.
BD.
试题解析:
CE=![]() BD.理由如下:
BD.理由如下:
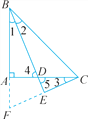
延长CE交BA的延长线于点F,如图
∵BE平分∠ABC,∴∠1=∠2.
∵CE⊥BD,
∴∠BEC=∠BEF=90°.
又∵BE=BE,
∴△BEC≌△BEF(ASA).
∴CE=FE=![]() CF.
CF.
∵∠1+∠4=∠3+∠5=90°,∠4=∠5,
∴∠1=∠3.
又∵∠BAD=∠CAF=90°,AB=AC,
∴△BAD≌△CAF(ASA),
∴BD=CF,
∴CE=![]() CF=
CF=![]() BD.
BD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目