题目内容
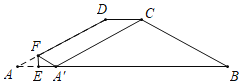
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连接AD(AD<AB),将线段AD绕点A逆时针旋转90°得到线段AE,连接DE,CE,BD.
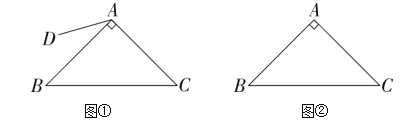
(1)请根据题意补全图①;
(2)猜测BD和CE的数量关系并证明;
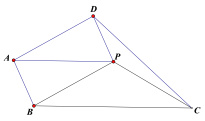
(3)作射线BD,CE交于点P,把△ADE饶点A旋转,当∠EAC=90°,AB=3,AD=2时,补全图形,直接写出PB的长.
【答案】(1)见解析;
(2)BD和CE的数量是:BD=CE;理由见解析;
(3)图见解析;PB的长是![]() 或
或![]() .
.
【解析】
(1)根据旋转的定义即可补全图形;
(2)根据题意证明△ABD≌△ACE即可解决问题;
(3)①根据题意证明△ACE≌△ABD,得到∠ACE=∠ABD,再根据两角对应相等得到△BPE∽△BAD,再根据对应线段成比例即可求解;②同理△BPE∽△BAD,求出
解:(1)补全图,如图;

(2)BD和CE的数量是:BD=CE;
∵∠DAB+∠BAE=∠CAE+∠BAE=90°,
∴∠DAB=∠CAE,
∵AD=AE,AB=AC,
∴△ABD≌△ACE,
∴BD=CE;
(3)结论:PB的长是.![]() 或
或![]()
理由:①如图②
由△ACE≌△ABD,可知:∠ACE=∠ABD,
∵∠AEC=∠BEP,
∴∠BPE=∠EAC=90°,
∵∠PBE=∠ABD,
∴△BPE∽△BAD,
∴![]() ,
,
∵AB=AC=3,AD=AE=2,∴BE=AB-AE=AB-AD=1,
BD=EC=![]() =
=![]()
∴![]()
∴BP=![]()
②如图③,同理△BPE∽△BAD,
∴![]() ,
,
∵AB=AC=3,AD=AE=2,∴BE=AB+AE=AB+AD=5,
BD=EC=![]() =
=![]()
∴![]()
∴.BP=![]()

练习册系列答案
相关题目