Question

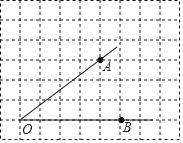
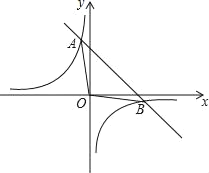
【题目】如图，在平面直角坐标系xOy中，点A在x轴上，点B在第一象限内，∠OAB＝90°，OA＝AB，△OAB的面积为2，反比例函数y＝的图象经过点B．

（1）求k的值；

（2）已知点P坐标为（a，0），过点P作直线OB的垂线l，点O，A关于直线l的对称点分别为O′，A′，若线段O′A′与反比例函数y＝的图象有公共点，直接写出a的取值范围．

Answer 1

【答案】（1）k＝4；（2）﹣2≤a≤1﹣ 或 2≤a≤1+

【解析】

（1）运用反比例函数的几何意义，求出k＝4；

（2）运用对称的点坐标关系，分别表示O′、A′，在第三象限，当点O′在双曲线上时a取最小值，当点A′在双曲线上时，a取最大值；在第一象限，同理可求a的取值范围

解：（1）∵∠OAB＝90°，OA＝AB，

∴设点B的坐标为（m，m），则OA＝AB＝m，

∵△OAB的面积为2，

∴＝2，

解得：m＝2（负值舍去），

∴点B的坐标为（2，2），

代入反比例函数y＝中，得k＝4；

（2）∵B（2，2）

∴∠BOA＝45°，

∵l⊥OB，

∴O′A′⊥x轴

∴P、O′、A′三点共线，且点O′在直线OB上

∴O′（a，a）、A′（a，a﹣2）

当O′在反比例函数图象上时，有a×a＝4

解得：a1＝﹣2，a2＝2

当A′在反比例函数图象上时，有a×（a﹣2）＝4

解得：a3＝1+，a4＝1﹣

若线段O′A′与反比例函数y＝的图象有公共点，

a的取值范围是：﹣2≤a≤1﹣ 或 2≤a≤1+