题目内容
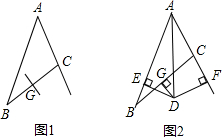 如图1,在△ABC中,BC的垂直平分线交BC于G,
如图1,在△ABC中,BC的垂直平分线交BC于G,(1)完成图形:在图1中,用直尺和圆规作∠BAC的平分线AD交BC的垂直平分线于点D(保留作图痕迹,不写作法)
(2)若在图1的基础上再作DE⊥AB于点E,DF⊥AC于点F,得到如图2,证明:BE=CF.
分析:(1)根据角平分线的作法,作出∠BAC的平分线AD即可;
(2)利用角平分线的性质以及垂直平分线的性质得出ED=DF,BD=CD,再利用HL定理得出Rt△EDB≌Rt△FDC,即BE=CF.
(2)利用角平分线的性质以及垂直平分线的性质得出ED=DF,BD=CD,再利用HL定理得出Rt△EDB≌Rt△FDC,即BE=CF.
解答: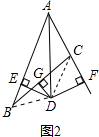
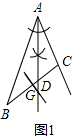 (1)解:如图1所示:
(1)解:如图1所示:
(2)如图2所示:
证明:∵BC的垂直平分线交BC于G,
∴BD=CD,
∵∠BAC的平分线AD交BC的垂直平分线于点D,
ED⊥AB,DF⊥AC,
∴ED=DF,
在Rt△EDB和Rt△FDC中,
∵
,
∴Rt△EDB≌Rt△FDC(HL),
∴BE=CF.

 (1)解:如图1所示:
(1)解:如图1所示:(2)如图2所示:
证明:∵BC的垂直平分线交BC于G,
∴BD=CD,
∵∠BAC的平分线AD交BC的垂直平分线于点D,
ED⊥AB,DF⊥AC,
∴ED=DF,
在Rt△EDB和Rt△FDC中,
∵
|
∴Rt△EDB≌Rt△FDC(HL),
∴BE=CF.
点评:此题主要考查了角平分线的作法以及垂直平分线的性质、全等三角形的判定等知识,熟练利用垂直平分线的性质以及角平分线的性质得出是解题关键.

练习册系列答案
相关题目

 明理由.
明理由.
 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=