题目内容
已知:如图1,在△ABC中,AB=AC,点D是边BC的中点.以BD为直径作圆O,交边AB于点P,连接PC,交AD于点E.(1)求证:AD是圆O的切线;
(2)当∠BAC=90°时,求证:
| PE |
| CE |
| 1 |
| 2 |
(3)如图2,当PC是圆O的切线,E为AD中点,BC=8,求AD的长.

分析:(1)要证明AD是圆O的切线,只要证明∠BDA=90°即可;
(2)连接PD、PO,根据直径上的圆周角是直角可得PD∥AC,所以得△PBD是等腰三角形,则OD=
BD,又由已知得OD=
BD=
DC,由平行线分线段成比例得
=
;
(3)连接OP,根据三角函数可求得PC,CD的长,再在RT△ADE中利用三角函数求得DE的长,进而得出AD的长.
(2)连接PD、PO,根据直径上的圆周角是直角可得PD∥AC,所以得△PBD是等腰三角形,则OD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| PE |
| CE |
| 1 |
| 2 |
(3)连接OP,根据三角函数可求得PC,CD的长,再在RT△ADE中利用三角函数求得DE的长,进而得出AD的长.
解答: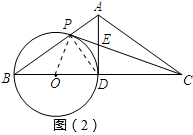 (1)证明:∵AB=AC,点D是边BC的中点,
(1)证明:∵AB=AC,点D是边BC的中点,
∴AD⊥BD.
又∵BD是圆O直径,
∴AD是圆O的切线.
(2)证明:连接PD、PO,
∴PD∥AC,
已知△ABC中,AB=AC,∴BD=DC,
∴PB=PD,
∴OD=OB=
BD=
DC,
∴PE=
CE,
∴
=
;
(3)解:连接OP,
由BC=8,得CD=4,OC=6,OP=2,
∵PC是圆O的切线,O为圆心,
∴∠OPC=90°.∴由勾股定理,得PC=4
,
在△OPC中,tan∠OCP=
=
,
在△DEC中,tan∠DCE=
=
,DE=DC•
=
.
∵E为AD中点,
∴AD=2
.
 (1)证明:∵AB=AC,点D是边BC的中点,
(1)证明:∵AB=AC,点D是边BC的中点,∴AD⊥BD.
又∵BD是圆O直径,
∴AD是圆O的切线.
(2)证明:连接PD、PO,
∴PD∥AC,
已知△ABC中,AB=AC,∴BD=DC,
∴PB=PD,
∴OD=OB=
| 1 |
| 2 |
| 1 |
| 2 |
∴PE=
| 1 |
| 2 |
∴
| PE |
| CE |
| 1 |
| 2 |
(3)解:连接OP,
由BC=8,得CD=4,OC=6,OP=2,
∵PC是圆O的切线,O为圆心,
∴∠OPC=90°.∴由勾股定理,得PC=4
| 2 |
在△OPC中,tan∠OCP=
| OP |
| CP |
| ||
| 4 |
在△DEC中,tan∠DCE=
| DE |
| DC |
| ||
| 4 |
| ||
| 4 |
| 2 |
∵E为AD中点,
∴AD=2
| 2 |
点评:此题考查学生对切线的判定及综合解直角三角形的能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目