题目内容
如图1,在△ABC中,∠BAC的平分线AD与∠BCA的平分线CE交于点O.
(1)求证:∠AOC=90°+
∠ABC;
(2)当∠ABC=90°时,且AO=3OD(如图2),判断线段AE,CD,AC之间的数量关系,并加以证明.

(1)求证:∠AOC=90°+
| 1 | 2 |
(2)当∠ABC=90°时,且AO=3OD(如图2),判断线段AE,CD,AC之间的数量关系,并加以证明.

分析:(1)求出∠BAC+∠BCA=180°-∠ABC,根据角平分线定义求出∠OAC=
∠BAC,∠OCA=
∠BCA,即可求出∠OAC+∠OCA的度数,根据三角形内角和定理求出即可.
(2)在AC上分别截取AM、CN,使AM=AE,CN=CD,连接OM,ON,证△AEO≌△AMO,△DCO≌△NCO,推出∠EOA=∠MOA,∠CON=∠COD,OD=ON,求出∠MON=∠MOA=45°,根据角平分线性质求出MK=ML,根据S△AOM=
AO×MK,S△MON=
ON×ML求出
=
,求出
=
=
,推出AN=
AM=
AE即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)在AC上分别截取AM、CN,使AM=AE,CN=CD,连接OM,ON,证△AEO≌△AMO,△DCO≌△NCO,推出∠EOA=∠MOA,∠CON=∠COD,OD=ON,求出∠MON=∠MOA=45°,根据角平分线性质求出MK=ML,根据S△AOM=
| 1 |
| 2 |
| 1 |
| 2 |
| AO |
| ON |
| AM |
| MN |
| AO |
| ON |
| AM |
| MN |
| 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
解答:(1)证明:∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC+∠BCA=180°-∠ABC,
∵∠BAC的平分线AD与∠BCA的平分线CE交于点O.
∴∠OAC=
∠BAC,∠OCA=
∠BCA,
∴∠OAC+∠OCA=
(∠BAC+∠BCA)=
(180°-∠ABC)=90°-
∠ABC,
∴∠AOC=180°-(∠OAC+∠OCA)=180°-(90°-
∠ABC),
即∠AOC=90°+
∠ABC.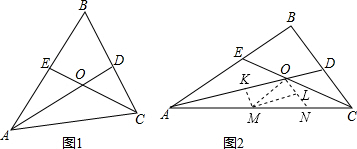
(2)
AE+CD=AC,
证明:∵∠AOC=90°+
∠ABC=135°,
∴∠EOA=45°,
在AC上分别截取AM、CN,使AM=AE,CN=CD,连接OM,ON,
则在△AEO和△AMO中
∴△AEO≌△AMO,
同理△DCO≌△NCO,
∴∠EOA=∠MOA,∠CON=∠COD,OD=ON,
∴∠EOA=∠MOA=∠CON=∠COD=45°,
∴∠MON=∠MOA=45°,
过M作MK⊥AD于K,ML⊥ON于L,
∴MK=ML,
S△AOM=
AO×MK,S△MON=
ON×ML,
∴
=
,
∵
=
,
∴
=
,
∵AO=3OD,
∴
=
,
∴
=
=
,
∴AN=
AM=
AE,
∵AN+NC=AC,
∴
AE+CD=AC.
∴∠BAC+∠BCA=180°-∠ABC,
∵∠BAC的平分线AD与∠BCA的平分线CE交于点O.
∴∠OAC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OAC+∠OCA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AOC=180°-(∠OAC+∠OCA)=180°-(90°-
| 1 |
| 2 |
即∠AOC=90°+
| 1 |
| 2 |

(2)
| 4 |
| 3 |
证明:∵∠AOC=90°+
| 1 |
| 2 |
∴∠EOA=45°,
在AC上分别截取AM、CN,使AM=AE,CN=CD,连接OM,ON,
则在△AEO和△AMO中
|
∴△AEO≌△AMO,
同理△DCO≌△NCO,
∴∠EOA=∠MOA,∠CON=∠COD,OD=ON,
∴∠EOA=∠MOA=∠CON=∠COD=45°,
∴∠MON=∠MOA=45°,
过M作MK⊥AD于K,ML⊥ON于L,
∴MK=ML,
S△AOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AO |
| ON |
| S△AOM |
| S△MON |
∵
| S△AOM |
| S△MON |
| AM |
| MN |
∴
| AO |
| ON |
| AM |
| MN |
∵AO=3OD,
∴
| AO |
| OD |
| 3 |
| 1 |
∴
| AO |
| ON |
| AM |
| MN |
| 3 |
| 1 |
∴AN=
| 4 |
| 3 |
| 4 |
| 3 |
∵AN+NC=AC,
∴
| 4 |
| 3 |
点评:本题考查了全等三角形的性质和判定,角平分线定义和性质,三角形的面积,三角形内角和定理的应用,题目比较好,综合性比较强,难度偏大.

练习册系列答案
相关题目

 明理由.
明理由.
 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=