题目内容
【题目】如图,点A是双曲线![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,四边形ACBD是以AB为对角线的正方形,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图像上运动,则这个函数的解析式是________.
在第一象限上的一动点,连接AO并延长交另一分支于点B,四边形ACBD是以AB为对角线的正方形,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图像上运动,则这个函数的解析式是________.

【答案】![]()
【解析】
过点C作CE⊥x轴于E,过A作AF⊥x轴于F,连接OC,设点A坐标为(a,![]() ),由A点、B点是正比例函数图象与双曲线y=
),由A点、B点是正比例函数图象与双曲线y=![]() 的交点可得A、B关于原点对称,可得OA=OB,由正方形的性质可得OC⊥AB,根据直角三角形两锐角互余的关系及平角的定义可得∠OCE=∠AOF,进而可证明△OCE≌△AOF,可得OE=AF,CE=OF,即可得C点坐标根据反比例函数的定义即可得答案.
的交点可得A、B关于原点对称,可得OA=OB,由正方形的性质可得OC⊥AB,根据直角三角形两锐角互余的关系及平角的定义可得∠OCE=∠AOF,进而可证明△OCE≌△AOF,可得OE=AF,CE=OF,即可得C点坐标根据反比例函数的定义即可得答案.
如图,过点C作CE⊥x轴于E,过A作AF⊥x轴于F,连接OC,
设点A坐标为(a,![]() ),
),
∴AF=![]() ,OF=a,
,OF=a,
∵A点、B点是正比例函数图象与双曲线y=![]() 的交点,
的交点,
∴点A与点B关于原点对称,
∴OA=OB,
∵四边形ACBD是正方形,
∴OC⊥AB,OC=OA=OB,
∴∠COE+∠AOF=90°,
∵∠OCE+∠COE=90°,
∴∠OCE=∠AOF,
在△OCE和△AOF中,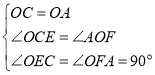 ,
,
∴△OCE≌△AOF,
∴CE=OF=a,OE=AF=![]() ,
,
∴点C坐标为(-![]() ,a),
,a),
∵-![]()
![]() a=-6,
a=-6,
∴点C在反比例函数y=-![]() 图象上.
图象上.
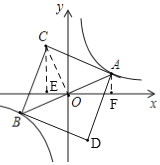
故答案为:y=-![]()

练习册系列答案
相关题目
【题目】如表是某校七~九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同.
课外小组活动总时间/h | 文艺小组活动次数 | 科技小组活动次数 | |
七年级 | 12.5 | 4 | 3 |
八年级 | 10.5 | 3 | 3 |
九年级 | 7 | ☆ | ☆ |
则九年级文艺小组活动次数和科技小组活动次数(表中的两个五星)分别是( )
A.2,2B.1,3C.3,1D.1,2