题目内容
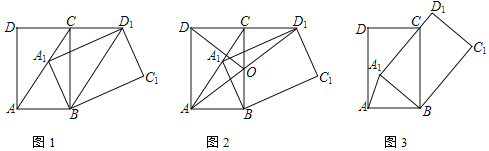
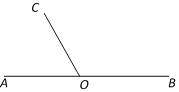
【题目】如图1,点![]() 为直线AB上一点,过O点作射线
为直线AB上一点,过O点作射线![]() ,使
,使![]() ,将一直角三角板的直角顶点放在点
,将一直角三角板的直角顶点放在点![]() 处,一边OM在射线OB上,另一边ON在直线AB的下方.
处,一边OM在射线OB上,另一边ON在直线AB的下方.
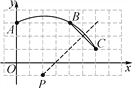
(1)将图1中的三角板绕点![]() 按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为_______度.
按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为_______度.

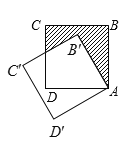
(2)继续将图2中的三角板绕点![]() 按逆时针方向旋转至图3的位置,使得ON在
按逆时针方向旋转至图3的位置,使得ON在![]() 的内部.试探究
的内部.试探究![]() 与
与![]() 之间满足什么等量关系,并说明理由;
之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1开始绕点O按![]() 每秒的速度逆时针旋转
每秒的速度逆时针旋转![]() 的过程中, 是否存在
的过程中, 是否存在![]() 所在直线平分
所在直线平分![]() 和
和![]() 中的一个角,ON所在直线平分另一个角?若存在,直接写出旋转时间
中的一个角,ON所在直线平分另一个角?若存在,直接写出旋转时间![]() ,若不存在,说明理由.
,若不存在,说明理由.
【答案】(1)90;(2)∠AOM∠NOC=30°,理由见解析;(3)存在,2秒或5秒或8秒.
【解析】
(1)根据旋转的性质可知,旋转角为∠MON;
(2)如图3,利用平角的定义,结合已知条件:∠AOC:∠BOC=1:2,求得∠AOC=60°,然后由直角的性质、图中角与角的数量关系推知∠AOM∠NOC=30°;
(3)需要分类讨论:当OM平分∠BOC时,旋转角是60°;当ON平分∠AOC时,旋转角为240°.
解:(1)根据旋转的性质可知:
旋转角为∠MON=90°.
故答案为:90.
(2)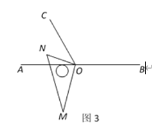
如图3:∠AOM∠NOC=30°,理由如下:
∵∠AOC+∠BOC=180°,
∠AOC:∠BOC=1:2,
∴∠AOC+2∠AOC=180°,
∴∠AOC=60°,
∴∠AON+∠CON=60°,①
∵∠MON=90°,
∴∠AOM+∠AON=90°,②
②①,得∠AOM∠CON=30°.
(3)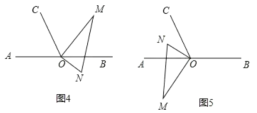
如图4,当OM平分∠BOC时,ON所在直线平分∠AOC,
∠BOM=60°,
∴三角板绕点O逆时针旋转60°,
此时t=60÷30=2(秒);
如图5,当ON平分∠AOC时,OM所在直线平分∠BOC,
∠CON=30°,
∴三角板绕点O逆时针旋转240°,
此时t=240÷30=8(秒).
当OM旋转150度时也符合要求,此时旋转了5秒.
答:旋转时间为2秒或5秒或8秒.

【题目】成都华联商场经销甲、乙两种商品,甲种商品每件进价150元,售价200元;乙种商品每件进价350元,售价450元.
(1)该商场在“十一”黄金周期间销售甲、乙两种商品共100件,销售额为35000元,求甲、乙两种商品各销售了多少件?
(2)假若该商场在“十一”黄金周期间销售甲、乙两种商品进行如下优惠活动:
打折前一次性购物总金额 | 优惠措施 |
不超过3000元 | 不优惠 |
超过3000元且不超过4000元 | 总售价打九折 |
超过4000元 | 总售价打八折 |
按上述优惠条件,若小王第一天只购买甲种商品一次性付款2000元,第二天只购买乙种商品打折后一次性付款3240元,那么这两天他在该商场购买甲、乙两种商品一共多少件?