题目内容
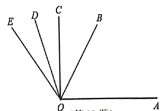
【题目】如图，已知：OB是∠AOE的平分线，OD是∠COE的平分线.
（1）若∠AOC＝ 90°，∠COE ＝30°，求∠BOD的度数；
（2）若（1）中的∠COE=α（α为锐角），其它条件不变，求∠BOD的度数；
（3）若（1）中的∠AOC=β，其它条件不变，求∠BOD的度数；
（4）从（1），（2），（3）的结果中猜想∠BOD与∠AOC的数量关系是________ ，并说明理由.
【答案】(1) 45°；(2) 45°；(3)
β；(4) ∠BOD=∠AOC，理由见详解.
【解析】
（1）求出∠AOE，根据角平分线定义得出∠BOE=∠AOE，∠DOE=∠COE，代入求出∠BOE和∠DOE度数，根据∠BOD=∠BOE-∠DOE，代入求出即可；
（2）求出∠AOE，根据角平分线定义得出∠BOE=∠AOE，∠DOE=∠COE，代入求出∠BOE和∠DOE度数，根据∠BOD=∠BOE-∠DOE，代入求出即可；
（3）求出∠AOE，根据角平分线定义得出∠BOE=∠AOE，∠DOE=∠COE，代入求出∠BOE和∠DOE度数，根据∠BOD=∠BOE-∠DOE，代入求出即可；
（4）设∠AOC=α，∠COE=β，求出∠AOE，根据角平分线定义得出∠BOE=∠AOE，∠DOE=∠COE，代入求出∠BOE和∠DOE度数，根据∠BOD=∠BOE-∠DOE，代入求出即可．
(1)∵∠AOC=90°,∠COE=30°，
∴∠AOE=∠AOC+∠COE=120°，
∵OB是∠AOE的平分线，OD是∠COE的平分线，
∴∠BOE=∠AOE=60°,∠DOE=∠COE=15°，
∴∠BOD=∠BOE∠DOE=60°15°=45°
(2)∵∠AOC=60°，∠COE=α，
∴∠AOE=∠AOC+∠COE=90°+α，
∵OB是∠AOE的平分线，OD是∠COE的平分线，
∴∠BOE=∠AOE= (90°+α),∠DOE=∠COE=α，
∴∠BOD=∠BOE∠DOE=
(90°+α)α=45°
(3)∵∠AOC=β,∠COE=30°，
∴∠AOE=∠AOC+∠COE=β+30°，
∵OB是∠AOE的平分线，OD是∠COE的平分线，
∴∠BOE=∠AOE=(β+30°),∠DOE=∠COE=15°，
∴∠BOD=∠BOE∠DOE= (β+30°) 15°=β.
(4)∠BOD=∠AOC，
理由是：设∠AOC=α，∠COE=β，
则∠AOE=∠AOC+∠COE=α+β，
∵OB是∠AOE的平分线，OD是∠COE的平分线，
∴∠BOE=(α+β),∠DOE=∠COE=β，
∴∠BOD=∠BOE∠DOE= (α+β)β=α，
∵∠AOC=α，
∴∠BOD=∠AOC.
