题目内容
【题目】如图,已知ΔABC内接于⊙O,AB为⊙O的直径,BD⊥AB,交AC的延长线于点D.
(1)若E是BD的中点,连结CE,试判断CE与⊙O的位置关系.
(2)若AC=3CD,求∠A的大小.

【答案】(1)位置关系:CE是⊙O的切线;(2)30°.
【解析】分析:(1)连接OC,利用思路:连半径,通过角的变换,证明出CO与CE的垂直关系,即可得出结论。(2)用m表示出DC、AC,根据△ACB∽△BCD,得出一组等量关系,从而求出BC,再求出∠A的正切值,即可得出∠A=30。
详解:(1)位置关系:CE是⊙O的切线.
连接OC,
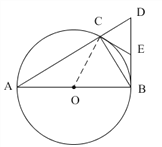
∵AB是⊙O的直径,
∴∠ACB=∠DCB=90°.
∵点E是BD的中点,
∴BE=CE.
∴∠EBC=∠ECB.
∵OC=OB
∴∠OCB=∠OBC
∴∠ECB+∠OCB=∠EBC+∠OBC
∴∠OCE=∠OBE.
∵BD⊥AB
∴∠OCE=∠OBE=90°
∴CE是⊙O的切线.
(2)∵∠ACB=∠BCD,∠A=∠DBC
∴ΔACB∽ΔBCD.
∴![]()
∴![]()
∵AC=3CD
∴![]() ,即
,即![]()
∴在RtΔACB中,tan∠A=![]()
∴∠A=30°.

练习册系列答案
相关题目



