题目内容
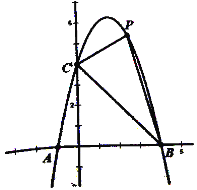
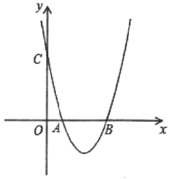
【题目】如图，已知抛物线的顶点为P（1，4），与y轴交于点C（0，3），与x轴交于点A，B．
（1）求此抛物线的解析式．
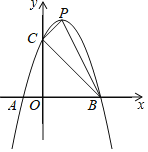
（2）设Q是直线BC上方该抛物线上除点P外的一点，且△BCQ与△BCP的面积相等，求点Q的坐标．
【答案】（1）y＝﹣x2+2x+3；（2）Q为（2，3）．
【解析】
（1）设顶点式y＝a（x﹣1）2+4（a≠0），然后把C点坐标代入可求出a，从而得到抛物线解析式；
（2）易得直线BC解析式为y＝﹣x+3，利用三角形面积公式可判断PQ∥BC，过P作PQ∥BC，交抛物线所得交点既为所求点Q．再求出直线PQ解析式为y＝﹣x+5，然后解方程组
，可得Q点坐标．
解：（1）抛物线的解析式为y＝a（x﹣1）2+4（a≠0），
把C（0，3）代入抛物线解析式得：a+4＝3，解得a＝﹣1，
∴抛物线解析式为y＝﹣（x﹣1）2+4，
即y＝﹣x2+2x+3；
（2）当y＝0时，﹣x2+2x+3＝0，解得x1＝﹣1，x2＝3，则B（3，0），
易得直线BC解析式为y＝﹣x+3，
∵S△PBC＝S△QBC，
∴PQ∥BC，
过P作PQ∥BC，交抛物线所得交点既为所求点Q．
∵P（1，4），
∴直线PQ解析式为y＝﹣x+5，
解方程组，
得：
或
，
∴Q为（2，3）．
练习册系列答案
相关题目
【题目】在二次函数y＝－x2＋bx＋c中，函数y与自变量x的部分对应值如下表：
x | …… | －2 | 0 | 3 | 4 | …… |
y | …… | －7 | m | n | －7 | …… |
则m、n的大小关系为( )
A. m＞n B. m＜n C. m＝n D. 无法确定
