题目内容
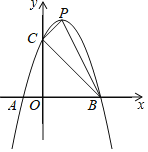
【题目】如图,二次函数y=x2+bx+c的图像与x轴交于A,B两点,B点坐标为(4,0),与y轴交于点C(0,4).点D为抛物线上一点
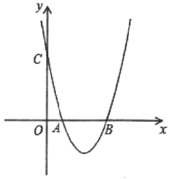
(1)求抛物线的解析式及A点坐标;
(2)若△BCD是以BC为直角边的直角三角形时,求点D的坐标;
(3)若△BCD是锐角三角形,请直接写出点D的横坐标m的取值范围 .
【答案】(1)y=x2-5x+4, A(1,0);(2)(6,10)或(2,-2);(3)3+![]() <m <6或 3-
<m <6或 3-![]() <m <2
<m <2
【解析】
(1)利用待定系数法求抛物线的解析式,再令y=0,求A的坐标;
(2)设D点横坐标为a,代入函数解析式可得纵坐标,分别讨论∠BCD=90°和∠CBD=90°的情况,作出图形进行求解;
(3)当BC为斜边构成Rt△BCD时,以BC中点O'为圆心,以BC为直径画圆,与抛物线交于D和D',此时△BCD和△BCD'就是以BC为斜边的直角三角形,利用两点间距离公式列出方程求解,然后结合(2)找到m的取值范围.
(1)将B(4,0),C(0,4)代入y=x2+bx+c得,
![]() ,解得
,解得![]() ,
,
所以抛物线的解析式为![]() ,
,
令y=0,得![]() ,解得
,解得![]() ,
,![]() ,
,
∴A点的坐标为(1,0)
(2)设D点横坐标为![]() ,则纵坐标为
,则纵坐标为![]() ,
,
①当∠BCD=90°时,如下图所示,连接BC,过C点作CD⊥BC与抛物线交于点D,过D作DE⊥y轴与点E,

由B、C坐标可知,OB=OC=4,
∴△OBC为等腰直角三角形,
∴∠OCB=∠OBC=45°,
又∵∠BCD=90°,
∴∠ECD+∠OCB=90°
∴∠ECD=45°,
∴△CDE为等腰直角三角形,
∴DE=CE=a
∴OE=OC+CE=a+4
由D、E纵坐标相等,可得![]() ,
,
解得![]() ,
,![]() ,
,
当![]() 时,D点坐标为(0,4),与C重合,不符合题意,舍去.
时,D点坐标为(0,4),与C重合,不符合题意,舍去.
当![]() 时,D点坐标为(6,10);
时,D点坐标为(6,10);
②当∠CBD=90°时,如下图所示,连接BC,过B点作BD⊥BC与抛物线交于点D,过B作FG⊥x轴,再过C作CF⊥FG于F,过D作DG⊥/span>FG于G,
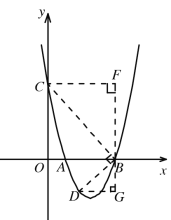
∵∠COB=∠OBF=∠BFC=90°,
∴四边形OBFC为矩形,
又∵OC=OB,
∴四边形OBFC为正方形,
∴∠CBF=45°
∵∠CBD=90°,
∴∠CBF+∠DBG=90°,
∴∠DBG=45°,
∴△DBG为等腰直角三角形,
∴DG=BG
∵D点横坐标为a,
∴DG=4-a,
而BG=![]()
∴![]()
解得![]() ,
,![]() ,
,
当![]() 时,D点坐标为(4,0),与B重合,不符合题意,舍去.
时,D点坐标为(4,0),与B重合,不符合题意,舍去.
当![]() 时,D点坐标为(2,-2);
时,D点坐标为(2,-2);
综上所述,D点坐标为(6,10)或(2,-2).
(3)当BC为斜边构成Rt△BCD时,如下图所示,以BC中点O'为圆心,以BC为直径画圆,与抛物线交于D和D',
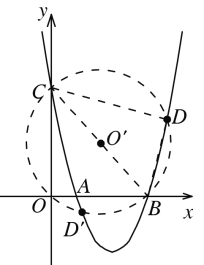
∵BC为圆O'的直径,
∴∠BDC=∠BD'C=90°,
∵![]() ,
,
∴D到O'的距离为圆O'的半径![]() ,
,
∵D点横坐标为m,纵坐标为![]() ,O'点坐标为(2,2),
,O'点坐标为(2,2),
∴![]()
即![]()
化简得:![]()
由图像易得m=0或4为方程的解,则方程左边必有因式![]() ,
,
∴采用因式分解法进行降次解方程
![]()
![]() 或
或![]() 或
或![]() ,
,
解得![]() ,
,![]() ,
,![]() ,
,![]()
当![]() 时,D点坐标为(0,4),与C点重合,舍去;
时,D点坐标为(0,4),与C点重合,舍去;
当![]() 时,D点坐标为(4,0),与B点重合,舍去;
时,D点坐标为(4,0),与B点重合,舍去;
当![]() 时,D点横坐标
时,D点横坐标![]() ;
;
当![]() 时,D点横坐标为
时,D点横坐标为![]() ;
;
结合(2)中△BCD形成直角三角形的情况,
可得△BCD为锐角三角形时,D点横坐标m的取值范围为3+![]() <m <6或 3-
<m <6或 3-![]() <m <2.
<m <2.

 阅读快车系列答案
阅读快车系列答案