Question

【题目】如图，抛物线经过，两点，与轴交于点.

（1）求抛物线的解析式；

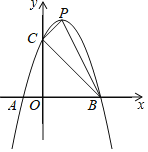
（2）若点在第一象限的抛物线上，且点的横坐标为，设的面积为，求与的函数关系式，并求的最大值；

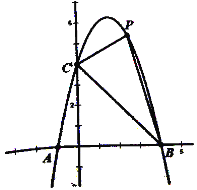
（3）在轴上是否存在点，使以点，，为顶点的三角形为等腰三角形？如果存在，直接写出点坐标；如果不存在，请说明理由.

Answer 1

【答案】（1）；（2），当时，的最大值为8；（3）存在. 或或，

【解析】

（1）抛物线y=ax2+3x+c经过A（-1，0），B（4，0），把A、B两点坐标代入上式，解得：a=-1，c=4，即可求解；

（2）如图所示，过点作的垂线，把代入抛物线的解析式，先求出C点坐标，把B，C代入抛物线方程，求出直线的解析式，再根据P点的横坐标为，得到，，PQ，根据三角形面积公式即可求出S；

（3）存在．分EC=BE、BC=CE、BC=BE分别求解即可．

解：（1）∵抛物线经过，，

把、两点坐标代入上式，解得：，，

故：抛物线；

（2）∵将代入抛物线的解析式得：，

∴，

把将，代入抛物线方程，

解得：直线的解析式为：.

过点作的垂线，如图所示：

∵点的横坐标为，

∴，.

∴.

∴.

∴当时，的最大值为8；

（3）存在. 如图所示：

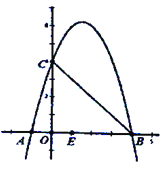
当时，在原点，此时点，

当时，在点关于轴对称点，此时点，

当时，，此时，，

即：或或，.