题目内容
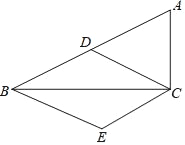
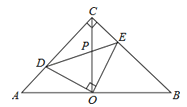
【题目】如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE;
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长;
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间数量关系,并说明理由.

【答案】(1)证明见解析;(2)![]() ;(3)线段AD、AB、CD之间数量关系:AD=AB+CD;理由见解析.
;(3)线段AD、AB、CD之间数量关系:AD=AB+CD;理由见解析.
【解析】
(1)先根据同角的余角相等可得:∠DEC=∠A,利用两角相等证明三角形相似;
(2)先根据勾股定理得:BE=3,根据△ABE∽△ECD,列比例式可得结论;
(3)先根据△AED∽△ECD,证明∠EAD=∠DEC,可得∠ADE=∠EDC,证明Rt△DFE≌Rt△DCE(HL),则DF=DC,同理可得:AF=AB,相加可得结论.
(1)证明:∵AB⊥BC,DC⊥BC,
∴∠B=∠C=90°,∠BAE+∠AEB=90°,
∵AE⊥DE,
∴∠AED=90°,
∴∠AEB+∠DEC=90°,
∴∠DEC=∠BAE,
∴△ABE∽△ECD;
(2)解:Rt△ABE中,∵AB=4,AE=5,
∴BE=3,
∵BC=5,
∴EC=5﹣3=2,
由(1)得:△ABE∽△ECD,
∴![]() ,
,
∴![]() ,
,
∴CD=![]() ;
;
(3)解:线段AD、AB、CD之间数量关系:AD=AB+CD;
理由是:过E作EF⊥AD于F,
∵△AED∽△ECD,
∴∠EAD=∠DEC,
∵∠AED=∠C,
∴∠ADE=∠EDC,
∵DC⊥BC,
∴EF=EC,
∵DE=DE,
∴Rt△DFE≌Rt△DCE(HL),
∴DF=DC,
同理可得:△ABE≌△AFD,
∴AF=AB,
∴AD=AF+DF=AB+CD.

练习册系列答案
相关题目