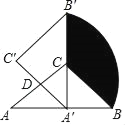
ЬтФПФкШн
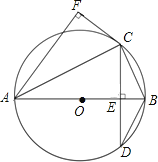
ЁОЬтФПЁПШчЭМХзЮяyЃНЉ![]() гыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЎCЃЌDСНЕуЙигкХзЮяЯпЖдГЦжсЖдГЦЃЌСЌНгBDНЛyжсгкЕуEЃЌХзЮяЯпЖдГЦжсНЛxжсгкЕуFЃЎ
гыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЎCЃЌDСНЕуЙигкХзЮяЯпЖдГЦжсЖдГЦЃЌСЌНгBDНЛyжсгкЕуEЃЌХзЮяЯпЖдГЦжсНЛxжсгкЕуFЃЎ
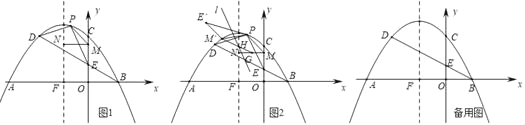
ЃЈ1ЃЉЕуPЮЊЯпЖЮBDЩЯЗНХзЮяЯпЩЯЕФвЛЕуЃЌСЌНгPDЃЌPEЃЎЕуMЪЧyжсЩЯвЛЕуЃЌЙ§ЕуMзїMNЁЭyжсНЛХзЮяЯпЖдГЦжсгкЕуNЃЎЕБЁїPDEУцЛ§зюДѓЪБЃЌЧѓPM+MN+![]() NFЕФзюаЁжЕЃЛ
NFЕФзюаЁжЕЃЛ
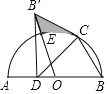
ЃЈ2ЃЉШчЭМ2ЃЌдкЃЈ1ЃЉжаPM+MN+![]() NFШЁЕУзюаЁжЕЪБЃЌНЋЁїPMEШЦЕуPЫГЪБеыа§зЊ120ЁуКѓЕУЕНЁїPMЁфEЁфЃЌЕуGЪЧMNЕФжаЕуЃЌСЌНгMЁфGНЛХзЮяЯпЕФЖдГЦжсгкЕуHЃЌЙ§ЕуHзїжБЯпlЁЮPMЃЌЕуRЪЧжБЯпlЩЯвЛЕуЃЌдкЦНУцжБНЧзјБъЯЕжаЪЧЗёДцдквЛЕуSЃЌЪЙвдЕуMЁфЃЌЕуGЃЌЕуRЃЌЕуSЮЊЖЅЕуЕФЫФБпаЮЪЧОиаЮЃПШєДцдкЃЌжБНгаДГіЕуSЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
NFШЁЕУзюаЁжЕЪБЃЌНЋЁїPMEШЦЕуPЫГЪБеыа§зЊ120ЁуКѓЕУЕНЁїPMЁфEЁфЃЌЕуGЪЧMNЕФжаЕуЃЌСЌНгMЁфGНЛХзЮяЯпЕФЖдГЦжсгкЕуHЃЌЙ§ЕуHзїжБЯпlЁЮPMЃЌЕуRЪЧжБЯпlЩЯвЛЕуЃЌдкЦНУцжБНЧзјБъЯЕжаЪЧЗёДцдквЛЕуSЃЌЪЙвдЕуMЁфЃЌЕуGЃЌЕуRЃЌЕуSЮЊЖЅЕуЕФЫФБпаЮЪЧОиаЮЃПШєДцдкЃЌжБНгаДГіЕуSЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉPM+MN+![]() NFЕФзюаЁжЕЃН
NFЕФзюаЁжЕЃН![]() ЃЛЃЈ2ЃЉДцдкЃЌЕуSЕФзјБъЮЊЃКS1ЃЈ
ЃЛЃЈ2ЃЉДцдкЃЌЕуSЕФзјБъЮЊЃКS1ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌS2ЃЈ
ЃЉЃЌS2ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉД§ЖЈЯЕЪ§ЗЈЧѓжБЯпBDНтЮіЪНЃЌдйИљОнЖўДЮКЏЪ§зюДѓжЕЗНЗЈЧѓЁїPDEУцЛ§зюДѓЪБЖдгІЕФЕуPзјБъЃЌзюКѓвРОнСНЕужЎМфЯпЖЮзюЖЬЧѓPM+MN+![]() NFЕФзюаЁжЕЃЛ
NFЕФзюаЁжЕЃЛ
ЃЈ2ЃЉгЩа§зЊЧѓЕуMЁфзјБъЃЌД§ЖЈЯЕЪ§ЗЈЧѓжБЯпPMНтЮіЪНЁЂжБЯпMЁфGвдМАжБЯпlЕФНтЮіЪНЃЌвРОнОиаЮаджЪЗжРрЬжТлЧѓRзјБъЃЌдйИљОнЦНвЦЙцТЩЧѓЯргІЕФSзјБъЃЎ
ЃЈ1ЃЉдкХзЮяЯпyЃНЉ![]() x2-
x2-![]() жаЃЌСюxЃН0ЃЌЕУЃКyЃН
жаЃЌСюxЃН0ЃЌЕУЃКyЃН![]() ЃЌСюyЃН0ЃЌЕУЃК
ЃЌСюyЃН0ЃЌЕУЃК
x1ЃНЉ3ЃЌx2ЃН1
ЁрAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌCЃЈ0ЃЌ![]() ЃЉ,
ЃЉ,
ЁпyЃНЉ![]() x2
x2![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЖдГЦжсЮЊЃКжБЯпxЃНЉ1
ЁрDЃЈЉ2ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЩшжБЯпBDНтЮіЪНЮЊyЃНkx+bЃЌНЋBЃЈ1ЃЌ0ЃЉЃЌDЃЈЉ2ЃЌ![]() ЃЉДњШыЕУ
ЃЉДњШыЕУ ЃЌ
ЃЌ
НтЕУЃК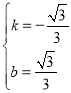
ЁржБЯпBDНтЮіЪНЮЊyЃН-![]() x+
x+![]()
ЁрEЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Й§ЕуPзїPGЁЭxжсгкGНЛBDгкHЃЌзїPQЁЭBDгкQЃЌСЌНгCDЃЌ
ЩшPЃЈmЃЌ-![]() m2-
m2-![]() +
+![]() ЃЉЃЌHЃЈmЃЌ-
ЃЉЃЌHЃЈmЃЌ-![]() m+
m+![]() ЃЉ
ЃЉ
PHЃН-![]() m2-
m2-![]() +
+![]()
ЁпPGЁЮyжс
ЁрЁЯPHDЃНЁЯDECЃЌ
ЁпCЁЂDЙигкжБЯпxЃНЉ1ЖдГЦЃЌ
ЁрЁЯDCEЃНЁЯPQEЃН90Ёу
ЁрЁїDCEЁзЁїHQP
Ёр![]() ЃЌМДЃКPQDEЃНDCPHЃЌ
ЃЌМДЃКPQDEЃНDCPHЃЌ
ЁрSЁїPDEЃН![]() PQDEЃН
PQDEЃН![]() DCPHЃН
DCPHЃН![]() ЁС2ЃЈ-
ЁС2ЃЈ-![]() m2-
m2-![]() +
+![]() ЃЉ
ЃЉ
ЃН-![]() ЃЌ
ЃЌ
Ёп-![]() ЃМ0,
ЃМ0,
ЁрЕБmЃНЉ![]() ЪБЃЌSЁїPDEЕФзюДѓжЕЃН
ЪБЃЌSЁїPDEЕФзюДѓжЕЃН![]() ЃЌДЫЪБЃЌPЃЈЉ
ЃЌДЫЪБЃЌPЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
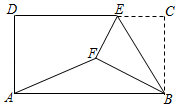
Й§ЕуFзїЁЯNFSЃН60ЁуЃЌЙ§NзїЁЯFNSЃН30ЁуЃЌFSгыNSНЛгкЕуSЃЌШчЭМЃЌ
ЁрЁЯFSNЃН90ЁуЃЌ
ЁрNSЃНNFcosЁЯFNSЃНNFcos30ЁуЃН![]() NFЃЌЙ§MзїMKЁЮNSЃЌЧвMKЃНNSЃЌ
NFЃЌЙ§MзїMKЁЮNSЃЌЧвMKЃНNSЃЌ
ЕБPЁЂMЁЂKШ§ЕуЙВЯпЪБЃЌPM+MKзюаЁЃЌ
ЁрЁЯPMCЃНЁЯKMEЃНЁЯFNSЃН30Ёу
ЁрPMЃН2PLЃН1ЃЌLMЃН![]() ЃЌMKЃНNSЃН
ЃЌMKЃНNSЃН![]() NFЃН
NFЃН![]() ЃЈ
ЃЈ![]() Љ
Љ![]() ЃЉЃН
ЃЉЃН![]() ЃЌMNЃН1
ЃЌMNЃН1
ЁрPM+MN+![]() NFЕФзюаЁжЕЃН1+1+
NFЕФзюаЁжЕЃН1+1+![]() ЃН
ЃН![]() .
.

ЃЈ2ЃЉШчЭМ:
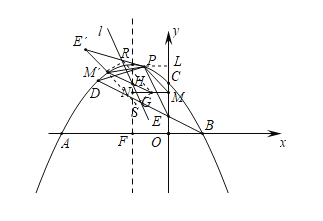
гЩЃЈ1ЃЉжЊЃКPЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌMЃЈ0ЃЌ
ЃЉЃЌMЃЈ0ЃЌ![]() ЃЉЃЌПЩЧѓЕУжБЯпPMНтЮіЪНЮЊЃКyЃН-
ЃЉЃЌПЩЧѓЕУжБЯпPMНтЮіЪНЮЊЃКyЃН-![]() x+
x+![]() ЃЌ
ЃЌ
ЁпЁЯPMLЃН30ЁуЃЌЁЯPLMЃН90ЁуЃЌЁрЁЯLPMЃН60Ёу
ЁпЁЯMPMЁфЃН120ЁуЃЌPMЁфЃНPMЃН1
ЁрMЁфЁЂPЁЂLШ§ЕуЙВЯпЃЌЁрMЁфЃЈ-![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпЕуGЪЧMNЕФжаЕуЃЌ
ЁрGЃЈ-![]() ЃЌ
ЃЌ![]() ЃЉЃЌД§ЖЈЯЕЪ§ЗЈПЩЧѓЕУжБЯпMЁфGЕФНтЮіЪНЮЊЃКyЃН-
ЃЉЃЌД§ЖЈЯЕЪ§ЗЈПЩЧѓЕУжБЯпMЁфGЕФНтЮіЪНЮЊЃКyЃН-![]() ЃЌСюxЃНЉ1ЃЌЕУyЃН
ЃЌСюxЃНЉ1ЃЌЕУyЃН![]()
ЁрHЃЈЉ1ЃЌ![]() ЃЉЃЌЁпжБЯпlЁЮPMЧвЙ§ЕуHЃЌ
ЃЉЃЌЁпжБЯпlЁЮPMЧвЙ§ЕуHЃЌ
ЁржБЯпlЕФНтЮіЪНЮЊЃКyЃН-![]() xЃЌЩшRЃЈtЃЌ-
xЃЌЩшRЃЈtЃЌ-![]() tЃЉЃЌЁпвдЕуMЁфЃЌЕуGЃЌЕуRЃЌЕуSЮЊЖЅЕуЕФЫФБпаЮЪЧОиаЮ
tЃЉЃЌЁпвдЕуMЁфЃЌЕуGЃЌЕуRЃЌЕуSЮЊЖЅЕуЕФЫФБпаЮЪЧОиаЮ
ЁрПЩвдЗжСНжжЧщаЮЃКMЁфGЮЊБпЛђMЁфGЮЊЖдНЧЯп
ЂйMЁфGЮЊБпЃЌЁЯRMЁфGЃН90ЁуЪБ
ЁрMЁфR2+MЁфH2ЃНRH2ЃЌМДЃК(t+ ЃНЃЈt+1ЃЉ2+(-
ЃНЃЈt+1ЃЉ2+(-![]() t-
t-![]() )2
)2
НтЕУЃКtЃН-![]() ЃЌ
ЃЌ
ЁрRЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌгЩЦНвЦПЩЕУS1ЃЈ-
ЃЉЃЌгЩЦНвЦПЩЕУS1ЃЈ-![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЂкMЁфGЮЊБпЃЌЁЯMЁфGRЃН90ЁуЪБ
ЁрGR2+HG2ЃНHR2ЃЌМДЃК(t+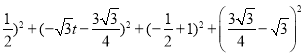 ЃНЃЈt+1ЃЉ2+(-
ЃНЃЈt+1ЃЉ2+(-![]() t-
t-![]() )2ЃЌ
)2ЃЌ
НтЕУЃКtЃН-![]() ЃЌ
ЃЌ
ЁрRЃЈ-![]() ЃЌ
ЃЌ![]() ЃЉЃЌгЩЦНвЦПЩЕУS2ЃЈ-
ЃЉЃЌгЩЦНвЦПЩЕУS2ЃЈ-![]() ЃЌ
ЃЌ![]() ЃЉ,
ЃЉ,
ЂлMЁфGЮЊЖдНЧЯпЃЌЁЯMЁфRGЃН90Ёу
ЁрMЁфR2+RG2ЃНMЁфG2ЃЌМДЃК(t+![]() )2+(-
)2+(-![]() -
-![]() )2+(t+
)2+(t+![]() )2+(-
)2+(-![]() ЃН(-
ЃН(-![]() ЃЌЮоНтЃЛ
ЃЌЮоНтЃЛ
злЩЯЫљЪіЃЌЕуSЕФзјБъЮЊЃКS1ЃЈ-![]() ЃЉЃЌS2ЃЈ-
ЃЉЃЌS2ЃЈ-![]() ЃЉЃЎ
ЃЉЃЎ

 ХргХШ§КУЩњЯЕСаД№АИ
ХргХШ§КУЩњЯЕСаД№АИ гХЛЏзївЕЩЯКЃПЦММЮФЯзГіАцЩчЯЕСаД№АИ
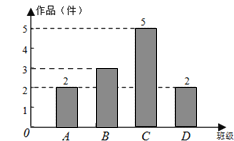
гХЛЏзївЕЩЯКЃПЦММЮФЯзГіАцЩчЯЕСаД№АИЁОЬтФПЁПЮЊСЫНјвЛВНСЫНтАЫФъМЖбЇЩњЕФЩэЬхЫижЪЧщПіЃЌЬхг§РЯЪІвдАЫФъМЖЃЈ1ЃЉАр50ЮЛбЇЩњЮЊбљБОНјааСЫвЛЗжжгЬјЩўДЮЪ§ВтЪдЃЎИљОнВтЪдНсЙћЃЌЛцжЦГіВПЗжЦЕЪ§ЗжВМБэКЭВПЗжЦЕЪ§ЗжВМжБЗНЭМЃЎ
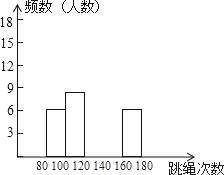
зщБ№ | ДЮЪ§x | ЦЕЪ§ЃЈШЫЪ§ЃЉ |
Ек1зщ | 80ЁмxЃМ100 | 6 |
Ек2зщ | 100ЁмxЃМ120 | 8 |
Ек3зщ | 120ЁмxЃМ140 | a |
Ек4зщ | 140ЁмxЃМ160 | 18 |
Ек5зщ | 160ЁмxЃМ180 | 6 |
ЧыНсКЯЭМБэЭъГЩЯТСаЮЪЬтЃК
ЃЈ1ЃЉБэжаЕФaЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧыАбЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉетИібљБОЪ§ОнЕФжаЮЛЪ§ТфдкЕкЁЁ ЁЁзщЃЛ
ЃЈ4ЃЉвбжЊИУаЃАЫФъМЖЙВгабЇЩњ800ЃЌЧыФуЙРМЦвЛЗжжгЬјЩўДЮЪ§ВЛЕЭгк120ДЮЕФАЫФъМЖбЇЩњДѓдМЖрЩйУћЃП