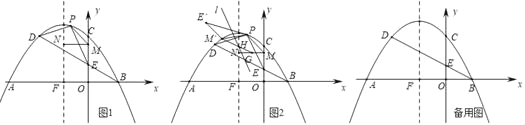
题目内容
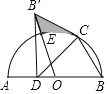
【题目】如图,以AB为直径,点O为圆心的半圆上有一点C,且∠ABC=60°,点D为AO上一点.将△DBC沿直线DC对折得到△DB'C,点B的对应点为B′,且B'C与半圆相切于点C,连接B′O交半圆于点E.
(1)求证:B'D⊥AB;
(2)当AB=2时,求图中阴影部分面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OC,根据切线的性质得到∠B'CO=90,根据等边三角形的性质、翻转变换的性质计算,得到∠B′DB=90°,证明结论;
(2)求出∠B′OC=45°,根据三角形的面积公式、扇形面积公式计算即可.
(1)证明:连接OC,
∵B'C与半圆相切于点C,
∴∠B'CO=90,
∵OC=OB,∠ABC=60°,
∴△OBC是等边三角形,
∴∠OCB=60°,∠B'CB=∠B'CO+∠OCB=90°+60°=150°,
∵△DBC沿直线DC对折得到△DB'C,
∴∠DCB=![]() ∠B’CB=
∠B’CB=![]() ×150°=75°,
×150°=75°,
在△DBC中,∠CDB=180°﹣∠ABC﹣∠DCB=180°﹣75°﹣60°=45°
∴∠B′DB=2∠CDB=2×45°=90°,
∴B′D⊥AB;
(2)解:∵AB=2,△OBC是等边三角形,
∴OC=OB=BC=B'C=1,
∵∠B'CO=90°,
∴∠B′OC=45°,
∴阴影部分的面积=S△B′OC﹣S扇形EOC=![]() B′CCO﹣
B′CCO﹣![]() =
=![]() ×1×1﹣
×1×1﹣![]() =
=![]() .
.


练习册系列答案
相关题目