题目内容
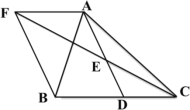
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A作BC的平行线交CE的延长线与F,且AF=BD,连接BF。
(1)求证:D是BC的中点;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论。
【答案】(1)详见解析;(2)详见解析
【解析】
(1)根据两直线平行,内错角相等求出∠AFE=∠DCE,然后利用“角角边”证明△AEF和△DEC全等,再根据全等三角形的性质和等量关系即可求解;
(2)由(1)知AF平行等于BD,易证四边形AFBD是平行四边形,而AB=AC,AD是中线,利用等腰三角形三线合一定理,可证AD⊥BC,即∠ADB=90°,那么可证四边形AFBD是矩形.
(1)证明:∵AF∥BC,
∴∠AFE=∠DCE,
∵点E为AD的中点,
∴AE=DE,
在△AEF和△DEC中,
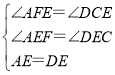 ,
,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∵AF=BD,
∴CD=BD,
∴D是BC的中点;
(2)若AB=AC,则四边形AFBD是矩形.理由如下:
∵△AEF≌△DEC,
∴AF=CD,
∵AF=BD,
∴CD=BD;
∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴∠ADB=90°,
∴平行四边形AFBD是矩形.

 名校课堂系列答案
名校课堂系列答案【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 6 |
第2组 | 30≤x<35 | 8 |
第3组 | 35≤x<40 | 16 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
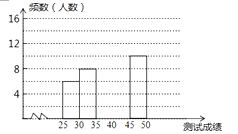
请结合图表完成下列各题:
(1)求表中a的值;(2)请把频数分布直方图补充完整;
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.