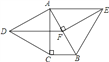
题目内容
【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.
,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.

【答案】(1)⊙O的半径OA的长为2;(2)阴影部分的面积为![]() .
.
【解析】试题分析: ![]() 连接OD.首先证明∠OCD=90°.构造直角三角形,运用勾股定理列出方程求解即可.
连接OD.首先证明∠OCD=90°.构造直角三角形,运用勾股定理列出方程求解即可.
![]() S阴影=S△CDO+S扇形OBD-S扇形OCE.
S阴影=S△CDO+S扇形OBD-S扇形OCE.
试题解析:(1)连接OD.∵OA⊥OB,
∴∠AOB=90°.
∵CD∥OB,
∴∠OCD=90°.
在Rt△OCD中,∵C是AO的中点, ![]()
∴OD=2OC.
设OC=x, ![]()
∴x=1,∴OD=2,
∴⊙O的半径为2;
(2) ![]()
∴∠CDO=30°.
∵FD∥OB,
∴∠DOB=∠CDO=30°,
∴S阴影=S△CDO+S扇形OBD-S扇形OCE![]()

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目