题目内容
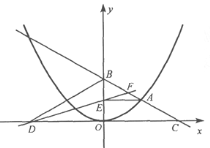
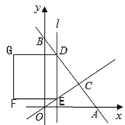
【题目】如图,直线![]() 分别于
分别于![]() 轴、
轴、![]() 轴交于A、B两点,与直线
轴交于A、B两点,与直线![]() 交于点C(2,4),平行于
交于点C(2,4),平行于![]() 轴的直线
轴的直线![]() 从原点
从原点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 轴向右平移,直线
轴向右平移,直线![]() 分别交直线AB、直线OC于点D、E,以DE为边向左侧作正方形DEFG,当直线
分别交直线AB、直线OC于点D、E,以DE为边向左侧作正方形DEFG,当直线![]() 经过点A时停止运动,设直线
经过点A时停止运动,设直线![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
(1)![]()
(2)设线段DE的长度为![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当正方形DEFG的边GF落在![]() 轴上,求出
轴上,求出![]() 的值;
的值;
(4)当![]() 时,若正方形DEFG和△OCB重叠部分面积为4,则
时,若正方形DEFG和△OCB重叠部分面积为4,则![]() 的值为________.
的值为________.
【答案】(1)b=8,k=2;(2)当t<2时,d=-4t+8;当t>2时,d=4x-8;(3)t=![]() ;(4)t=1.
;(4)t=1.
【解析】
(1)直接把点的坐标代入即可;(2)根据正方形性质和函数图象,分两种情况当t<2时;当t>2时;(3)设D(t,-2t+8),E(t,2t),DE=-4t+8;则 t=-4t+8;(4)由t(-4t+8)=4可得t.
解:(1)因为直线![]() 分别于
分别于![]() 轴、
轴、![]() 轴交于A、B两点,与直线
轴交于A、B两点,与直线![]() 交于点C(2,4),
交于点C(2,4),
所以![]() ,
,![]()
解得b=8,k=2;
(2)根据正方形性质,当t<2时,d=-4t+8;
当t>2时,d=4x-8;
(3)设D(t,-2t+8),E(t,2t),DE=-4t+8;
则 t=-4t+8,
解得t=![]() ;
;
(4)由t(-4t+8)=4,解得t=1.

 阅读快车系列答案
阅读快车系列答案【题目】某校为了解八年级学生课外阅读情况,随机抽取20名学生平均每周用于课外阅读读的时间(单位:![]() ),过程如下:
),过程如下:
(收集数据)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
(整理数据)
课外阅读时间 |
|
|
|
|
等级 |
|
|
|
|
人数 | 3 |
| 8 |
|
(分析数据)
平均数 | 中位数 | 众数 |
80 |
|
|
请根据以上提供的信息,解答下列问题:
(1)填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)如果每周用于课外读的时间不少于![]() 为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?
为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?
【题目】某班“数学兴趣小组”对函数y=![]() +x的图象与性质进行了探究,探究过程如下,请补充完整.
+x的图象与性质进行了探究,探究过程如下,请补充完整.
(1)函数y=![]() +x的自变量x的取值范围是 ;
+x的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | |
|
|
| 2 | 3 | 4 | 5 | … |
y | … | ﹣ | ﹣ | ﹣ | ﹣1 | ﹣ | ﹣ |
|
| 3 |
| m |
| … |
则m= ;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)该函数的图象关于点( , )成中心对称;
(5)直线y=m与该函数的图象无交点,则m的取值范围为 .