题目内容
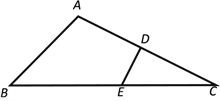
【题目】如图，已知△ABC中，∠B=45°，
，BC=6.
（1）求△ABC面积；
（2）AC的垂直平分线交AC于点D，交BC于点E. 求DE的长．
【答案】(1)6;(2) 
【解析】分析：（1）过点A作AH⊥BC于点H，根据题意得到三角形ACH为等腰直角三角形，设AH=BH=x，根据tanC的值，表示出HC，由BC=6求出x的值，确定出AH的长，即可求出三角形ABC面积；
（2）由（1）得到AH与CH的长，利用勾股定理求出AC的长，进而确定出CD的长，根据tanC的值，利用锐角三角函数定义求出DE的长即可．
详解：（1）过点A作AH⊥BC于点H．在Rt△ABC中，∠B=45°，设AH=x，则BH=x．在Rt△AHC中，tanC=
=
，∴HC=2x．∵BC=6，∴x+2x=6，解得：x=2，∴AH=2，∴S△ABC=BCAH=6；
（2）由（1）得AH=2，CH=4．在Rt△AHC中，AC=
=2
．∵DE垂直平分AC，∴CD=AC=．∵ED⊥AC，∴在Rt△EDC中，tanC=
=，∴DE=
．
练习册系列答案
相关题目
