题目内容
【题目】如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=![]() ∠A.
∠A.
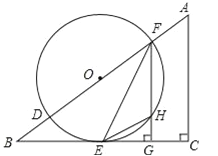
(1)求证:BC是⊙O的切线;
(2)若sinB=![]() ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
【答案】(1)证明过程见解析;(2)![]()
【解析】
试题分析:(1)首先连接OE,由在△ABC中,∠C=90°,FG⊥BC,可得FG∥AC,又由∠OFE=![]() ∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;(2)由在△OBE中,sinB=
∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;(2)由在△OBE中,sinB=![]() ,⊙O的半径为r,可求得OB,BE的长,然后由在△BFG中,求得BG,FG的长,则可求得EG的长,易证得△EGH∽△FGE,然后由相似三角形面积比等于相似比的平方,求得答案.
,⊙O的半径为r,可求得OB,BE的长,然后由在△BFG中,求得BG,FG的长,则可求得EG的长,易证得△EGH∽△FGE,然后由相似三角形面积比等于相似比的平方,求得答案.
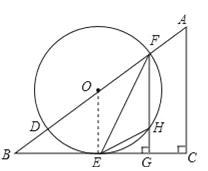
试题解析:(1)连接OE, ∵在△ABC中,∠C=90°,FG⊥BC, ∴∠BGF=∠C=90°, ∴FG∥AC,
∴∠OFG=∠A, ∴∠OFE=![]() ∠OFG, ∴∠OFE=∠EFG, ∵OE=OF, ∴∠OFE=∠OEF, ∴∠OEF=∠EFG,
∠OFG, ∴∠OFE=∠EFG, ∵OE=OF, ∴∠OFE=∠OEF, ∴∠OEF=∠EFG,
∴OE∥FG, ∴OE⊥BC, ∴BC是⊙O的切线;
(2)∵在Rt△OBE中,sinB=![]() ,⊙O的半径为r, ∴OB=
,⊙O的半径为r, ∴OB=![]() r,BE=
r,BE=![]() r, ∴BF=OB+OF=
r, ∴BF=OB+OF=![]() r,
r,
∴FG=BFsinB=![]() r, ∴BG=
r, ∴BG=![]() =
=![]() r, ∴EG=BG﹣BE=
r, ∴EG=BG﹣BE=![]() r,
r,
∴S△FGE=![]() EGFG=
EGFG=![]() r2,EG:FG=1:2, ∵BC是切线, ∴∠GEH=∠EFG, ∵∠EGH=∠FGE,
r2,EG:FG=1:2, ∵BC是切线, ∴∠GEH=∠EFG, ∵∠EGH=∠FGE,
∴△EGH∽△FGE, ∴![]() =(
=(![]() )=
)=![]() , ∴S△EHG=
, ∴S△EHG=![]() S△FGE=
S△FGE=![]() r2.
r2.

【题目】有这样一个问题:探究函数![]() 的图象与性质.小聪根据学习函数的经验,对函数
的图象与性质.小聪根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小聪的探究过程,请补充完整:
的图象与性质进行了探究.下面是小聪的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是____;
的取值范围是____;
(2)下表是![]() 与
与![]() 的几组对应值,请直接写出m的值,
的几组对应值,请直接写出m的值, ![]()
| … | -3 | -1.5 | -1 | 0 |
| 0.6 | 1.4 | 1.5 | 2 | 3 | 3.5 | 5 | … |
| … | 0.5 | 0.2 | 0 | -1 | -3 | -4 | 6 | 5 | 3 | 2 | 1.8 | 1.5 | … |
(3)请在平面直角坐标系xoy中,描出以上表中各组对应值为坐标的点,并画出该函数的图象.
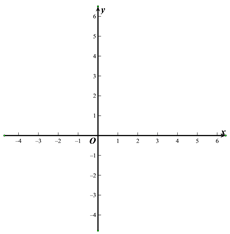
(4)结合函数图象,写出该函数的一条性质:
【题目】9岁的小芳身高1.36米,她的表姐明年想报考北京的大学.表姐的父母打算今年暑假带着小芳及其表姐先去北京旅游一趟,对北京有所了解.他们四人7月31日下午从无锡出发,1日到4日在北京旅游,8月5日上午返回无锡.
无锡与北京之间的火车票和飞机票价如下:火车 (高铁二等座) 全票524元,身高1.1~1.5米的儿童享受半价票;飞机 (普通舱) 全票1240元,已满2周岁未满12周岁的儿童享受半价票.他们往北京的开支预计如下:
住宿费 (2人一间的标准间) | 伙食费 | 市内交通费 | 旅游景点门票费 (身高超过1.2米全票) |
每间每天x元 | 每人每天100元 | 每人每天y元 | 每人每天120元 |
假设他们四人在北京的住宿费刚好等于上表所示其他三项费用之和,7月31日和8月5日合计按一天计算,不参观景点,但产生住宿、伙食、市内交通三项费用.
(1)他们往返都坐火车,结算下来本次旅游总共开支了13668元,求x,y的值;
(2)若去时坐火车,回来坐飞机,且飞机成人票打五五折,其他开支不变,他们准备了14000元,是否够用? 如果不够,他们准备不再增加开支,而是压缩住宿的费用,请问他们预定的标准间房价每天不能超过多少元?