题目内容
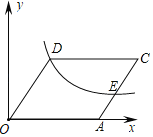
【题目】如图，在平面直角坐标系中，函数y＝
（x＞0）的图象经过菱形OACD的顶点D和边AC上的一点E，且CE＝2AE，菱形的边长为8，则k的值为_____．
【答案】3
【解析】
求出点D或点E的坐标，即可求出k的值，通过作垂线，利用三角形相似，和菱形的性质可以求出点 D 的坐标，进而求出k的值．
过点D、E分别作x轴的垂线，垂足为M、N，
∵ABCD是菱形，
∴OD＝AC＝OA＝8，OD∥AC，
∴∠DOA＝∠CAN，
∴△DOM∽△EAN，
∴
，
又∵CE＝2AE，
∴
，
设D（a，b），则OM＝a，DM＝b，
∴AN＝
a，EN＝b，
∴E（8+a，b）
又∵点D、点E都在函数y＝
（x＞0）的图象上，
∴ab＝（8+a）×b，
解得：a＝3，
在Rt△DOM中，b＝DM＝
＝，
∴k＝ab＝3，
故答案为：3
练习册系列答案
相关题目
【题目】在“五四青年节”来临之际，某校举办了以“我的青春我做主”为主题的演讲比赛． 并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计(等级：A：优秀，B：良好，C：一般，D：较差)，并制作了如下统计图表(部分信息未给出)：
等级 | 人数 |
A | m |
B | 20 |
C | n |
D | 10 |
请根据统计图表中的信息解答下列问题：
(1)这次共抽取了________名参加演讲比赛的学生，统计图中a＝________，b＝________；
(2)若该校学生共有2000人，如果都参加了演讲比赛，请你估计成绩达到优秀的有多少人？
(3)若演讲比赛成绩为A等级的学生中恰好有2名女生，其余的学生为男生，从A等级的学生中抽取两名同学参加全市演讲比赛，求抽中一名男生和一名女生的概率．
