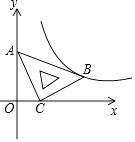Question

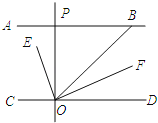
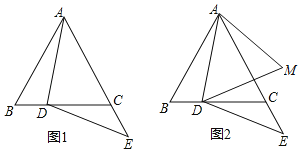
【题目】如图1，在△ABC中，BD⊥AC于点D．

（1）若∠C＝∠ABC＝2∠A，则∠DBC＝　 　°；

（2）若∠A＝2∠CBD，求证：∠ACB＝∠ABC；

（3）如图2，在（2）的条件下，E是AD上一点，F是AB延长线上一点，连接BE、CF，使∠BEC＝∠CFB，∠BCF＝2∠ABE，求∠EBC的度数．

Answer 1

【答案】（1）18；（2）见解析；（3）∠EBC＝60°.

【解析】

（1）由于∠C＝∠ABC＝2∠A＝2α，所以利用三角形内角和定理即可求出α的值，从而可求出∠DBC的值；

（2）由BD⊥AC，所以∠BDC＝∠ADB＝90°，所以∠DCB+∠DBC＝90°，∠A+∠ABD＝90°，所以∠ACB＝90°﹣∠DBC，∠ABD＝90°﹣∠A，所以∠ABD＝90°﹣2∠DBC，又易证∠ABC＝∠ABD+∠DBC＝90°﹣∠DBC，所以∠ACB＝∠ABC；

（3）由于∠ABC＝∠F+∠BCF，∠ABC＝∠ABE+∠EBC，∠BCF＝2∠ABE，所以∠EBC＝∠F+∠ABE，易证∠ACB＝2∠ABE+∠F，∠F+∠ABE+2∠ABE+∠F+∠F＝180°，从而可求出∠F+∠ABE＝60°，即∠EBC＝60°

解：（1）∵设∠A＝α

∴∠C＝∠ABC＝2α，

∴α+2α+2α＝180°，

∴α＝36°，

∴∠C＝2α＝72°，

∴∠DBC＝90°﹣∠C＝18°

（2）∵BD⊥AC，

∴∠BDC＝∠ADB＝90°，

∴∠DCB+∠DBC＝90°

∠A+∠ABD＝90°，

∴∠ACB＝90°﹣∠DBC

∠ABD＝90°﹣∠A，

∵∠A＝2∠DBC，

∴∠ABD＝90°﹣2∠DBC

∴∠ABC＝∠ABD+∠DBC

＝90°﹣2∠DBC+∠DBC

＝90°﹣∠DBC，

∴∠ACB＝∠ABC，

（3）∵∠ABC＝∠F+∠BCF

∠ABC＝∠ABE+∠EBC

∠BCF＝2∠ABE

∴∠EBC＝∠F+∠ABE，

∵∠ABC＝∠ACB，

∴∠ACB＝2∠ABE+∠F，

∵∠F＝∠BEC

∠EBC+∠ECB+∠BEC＝180°，

∴∠F+∠ABE+2∠ABE+∠F+∠F＝180°，

∴3∠F+3∠ABE＝180°，

∴∠F+∠ABE＝60°，

∴∠EBC＝60°