Question

【题目】某景区的三个景点A、B、C在同一线路上．甲、乙两名游客从景点A出发，甲步行到景点C;乙乘景区观光车先到景点B，在B处停留一段时间后，再步行到景点C，甲、乙两人同时到达景点C．甲、乙两人距景点A的路程y(米)与甲出发的时间x(分)之间的函数图象如图所示．

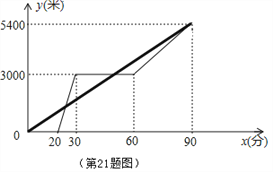
（1）乙步行的速度为_ __米/分．

（2）求乙乘景区观光车时y与x之间的函数关系式．

（3）甲出发多长时间与乙第一次相遇?

Answer 1

【答案】（1）80；（2）y＝30x-6000；（3）甲出发25分钟与乙第一次相遇．

【解析】试题分析：（1）根据速度=路程÷时间，即可求出乙步行的速度；

（2）观察函数图象，找出两点的坐标，利用待定系数即可求出乙乘景区观光车时y与x之间的函数关系式；

（3）根据速度=路程÷时间求出甲步行的速度，进而找出甲步行时y与x之间的函数关系式，联立两函数关系式成方程组，通过解方程组即可求出二者第一次相遇的时间．

试题解析：解：（1）乙步行的速度为：（5400﹣3000）÷（90﹣60）=80（米/分）．

故答案为：80．

（2）设乙乘景区观光车时y与x之间的函数关系式为y=kx+b（k≠0），将（20，0），（30，3000）代入y=kx+b得： ，解得： ，∴乙乘景区观光车时y与x之间的函数关系式为y=300x﹣6000（20≤x≤30）．

（3）甲步行的速度为：5400÷90=60（米/分），∴甲步行y与x之间的函数关系式为y=60x．

联立两函数关系式成方程组， ，解得： ，∴甲出发25分钟与乙第一次相遇．