题目内容
【题目】如图,在边长为2的正方形ABCD中,P是BC边上一动点(点P不与B、C重合),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA、NA,则以下结论:①△CMP∽△BPA;②四边形AMCB的面积最大值为2.5;③△ADN≌△AEN;④线段AM的最小值为2.5;⑤当P为BC中点时,AE为线段NP的中垂线.正确的有_____(只填序号)

【答案】①②③④
【解析】分析:①正确.只要证明∠CPM=∠PAB,∠C=∠B=90°,即可;
②正确,设PB=x,构建二次函数,利用二次函数性质解决问题即可;
③正确.根据HL即可证明;
④正确,作MG⊥AB于G,因为AM=![]() ,所以AG最小时AM最小,构建二次函数,求得AG的最小值为
,所以AG最小时AM最小,构建二次函数,求得AG的最小值为![]() ,AM的最小值为
,AM的最小值为![]() .
.
⑤错误,设ND=NE=y,在Rt△PCN中,利用勾股定理求出y即可解决问题.
详解:①由翻折可知,∠APE=∠APB,∠MPC=∠MPN,
∴∠APE+∠MPF=![]() ∠CPN+
∠CPN+![]() ∠BPE=90°,
∠BPE=90°,
∴∠CPM+∠APB=90°,∵∠APB+∠PAB=90°,
∴∠CPM=∠PAB,∵∠C=∠B=90°,
∴△CMP∽△BPA.故①正确;
②设PB=x,则CP=2-x,
∵△CMP∽△BPA,
∴![]() ,,
,,
∴CM=![]() x(2-x),
x(2-x),
∴S四边形AMCB=![]() [2+
[2+![]() x(2-x)]×2=-
x(2-x)]×2=-![]() x2+x+2=-
x2+x+2=-![]() (x-1)2+2.5,
(x-1)2+2.5,
∴x=1时,四边形AMCB面积最大值为2.5,故②正确;
③在Rt△ADN和Rt△AEN中,
![]() ,
,
∴△ADN≌△AEN.故③正确;
④作MG⊥AB于G,
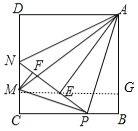
∵AM=![]() ,
,
∴AG最小时AM最小,
∵AG=AB-BG=AB-CM=2-![]() x(2-x)=
x(2-x)=![]() (x-1)2+
(x-1)2+![]() ,
,
∴x=1时,AG最小值=![]() ,
,
∴AM的最小值=![]() ,故④正确.
,故④正确.
⑤当PB=PC=PE=1时,
由折叠知,ND=NE,
设ND=NE=y,
在Rt△PCN中,(y+1)2=(2-y)2+12解得y=![]()
∴NE=![]() ,
,
∴NE≠EP,故⑤错误,

【题目】列方程式应用题.
天河食品公司收购了200吨新鲜柿子,保质期15天,该公司有两种加工技术,一种是加工为普通柿饼,另一种是加工为特级霜降柿饼,也可以不需加工直接销售.相关信息见表:
品种 | 每天可加工数量(吨) | 每吨获利(元) |
新鲜柿子 | 不需加工 | 1000元 |
普通柿饼 | 16吨 | 5000元 |
特级霜降柿饼 | 8吨 | 8000元 |
由于生产条件的限制,两种加工方式不能同时进行,为此公司研制了两种可行方案:
方案1:尽可能多地生产为特级霜降柿饼,没来得及加工的新鲜柿子,在市场上直接销售;
方案2:先将部分新鲜柿子加工为特级霜降柿饼,再将剩余的新鲜柿子加工为普通柿饼,恰好15天完成.
请问:哪种方案获利更多?获利多少元?