题目内容
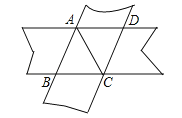
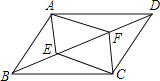
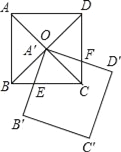
【题目】已知,如图,正方形ABCD的对角线AC,BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F.
(1)求证:OE=OF;
(2)若正方形ABCD的对角线长为4,求两个正方形重叠部分的面积为__.
【答案】2
【解析】分析:(1)由正方形的性质可以得出△BOE≌△COF,由全等三角形的性质就可以得出OE=OF;
(2)由全等可以得出S△BOE=S△COF,就可以得出S四边形OECF=S△BOC,S△BOC的面积就可以得出结论.
详解:(1)证明:∵正方形ABCD的对角线AC、BD交于点O
∴∠BOC=90°,∠OBC=∠OCD=∠OCF=45°,OB=OC,
∵正方形A'B'C'D'的A'B'交BC于点E,A'D'交CD于点F.
∴∠EOF=90°
∵∠BOE=∠EOF﹣∠EOC=90°﹣∠EOC
∠COF=∠BOC﹣∠EOC=90°﹣∠EOC
∴∠BOE=∠COF.
在△OBE和△OCF中,
∠BOE=∠COF,OB=OC,∠OBC=∠OCF,
∴△BOE≌△COF(ASA).
∴OE=OF;
(2)解:∵△BOE≌△COF,
∴S△BOE=S△COF
∴S△EOC+S△COF=S△EOC+S△BOE,
即S四边形OECF=S△BOC.
∵S△BOC=2,
∴两个正方形重叠部分的面积为2.
故答案为:2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目