题目内容
【题目】下面是小明设计的“分别以两条已知线段为腰和底边上的高作等腰三角形”的尺规作图过程．
已知：线段 a， b．
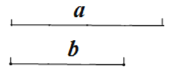
求作：等腰△ABC，使线段 a 为腰，线段 b 为底边 BC 上的高． 作法：如图，
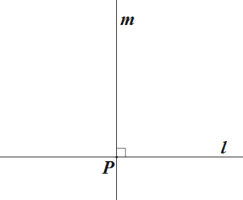
①画直线 l，作直线 m⊥l，垂足为 P；
②以点 P 为圆心，线段 b 的长为半径画弧，交直线 m 于点 A；
③以点 A 为圆心，线段 a 的长为半径画弧，交直线 l 于 B，C 两点；
④分别连接 AB， AC；
所以△ABC 就是所求作的等腰三角形． 根据小明设计的尺规作图过程，
（1）使用直尺和圆规，补全图形；（保留作图痕迹）
（2）完成下面的证明．
证明：∵ = ，
∴△ABC 为等腰三角形（ ）（填推理的依据）．
【答案】AB，AC；等腰三角形的定义
【解析】
（1）根据要求画出图形即可．
（2）根据等腰三角形的定义即可判断．
解：（1）如图，△ABC即为所求．
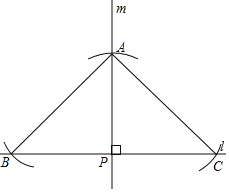
（2）∵AB＝AC，
∴△ABC是等腰三角形（等腰三角形的定义）
故答案为：AB，AC；等腰三角形的定义．
练习册系列答案
相关题目
