Question

【题目】如图，在等腰直角△ABC 中，∠ACB=90°，AC=BC，D 为 AB 中点，DE⊥DF.

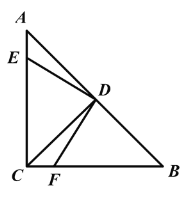
（1）图中有 对全等三角形；

（2）求证：ED=DF.

Answer 1

【答案】（1）3；（2）详见解析

【解析】

（1）利用等腰直角三角形的性质和三角形全等的判定解答即可；

（2）根据等腰直角三角形的性质和三角形全等的判定证明即可.

（1）∵△ABC是等腰直角三角形，且D为AB中点≌

∴CD⊥AB，且CD=BD=AD

∴∠A=∠B=∠ACD=∠BCD=45°

又∵DE⊥DF

∴∠EDF=∠ADC=∠CDB=90°，即∠ADE+∠EDC=∠CDF+∠EDC=∠CDF+∠FDB=90°

∴∠ADE =∠CDF, ∠EDC =∠FDB

由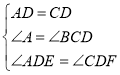 （AAS）得：AED≌CFD

∴ED=FD

由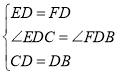（SAS）得：CED≌BFD

由（ASA）得：ACD≌BCD或ACD≌CBD

全等三角形有△AED≌CFD；CED≌BFD；ACD≌BCD或ACD≌CBD；

故答案为: 3

（2） AC BC，AD BD

CDA 90，FCD 45

AD CD

CDA ADEEDC

EDF CDFEDC

EDF CDA 90

ADE CDF

在AED与CFD中

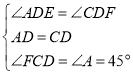
AED≌CFD

DE DF.