题目内容
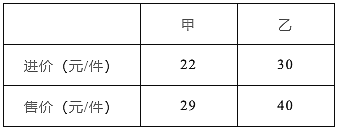
【题目】列方程解应用题:某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)
(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙种商品是按原价打几折销售?
【答案】(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获利1950元;(2)第二次乙种商品是按原价打![]() 折销售
折销售
【解析】
(1)设第一次购进甲商品x件,则购进乙商品(![]() x+15)件,根据题意列出方程即可求出x的值,然后根据“获利=售价-进价”即可求出结论;
x+15)件,根据题意列出方程即可求出x的值,然后根据“获利=售价-进价”即可求出结论;
(2)设第二次乙种商品是按原价打y折销售,根据题意列出方程即可求出结论.
解:(1)设第一次购进甲商品x件,则购进乙商品(![]() x+15)件
x+15)件
由题意可得:22x+30(![]() x+15)=6000
x+15)=6000
解得:x=150
∴购进乙商品![]() ×150+15=90件
×150+15=90件
∴全部卖完后一共可获利(29-22)×150+(40-30)×90=1950(元)
答:该超市将第一次购进的甲、乙两种商品全部卖完后一共可获利1950元.
(2)设第二次乙种商品是按原价打y折销售
由题意可得:(29-22)×150+(40×![]() -30)×90×3-1950=180
-30)×90×3-1950=180
解得:y=![]()
答:第二次乙种商品是按原价打![]() 折销售.
折销售.

练习册系列答案
相关题目