题目内容
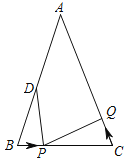
【题目】如图1,一次函数y=﹣x+b与反比例函数y= ![]() (k≠0)的图象交于点A(1,3),B(m,1),与x轴交于点D,直线OA与反比例函数y=
(k≠0)的图象交于点A(1,3),B(m,1),与x轴交于点D,直线OA与反比例函数y= ![]() (k≠0)的图象的另一支交于点C,过点B作直线l垂直于x轴,点E是点D关于直线l的对称点.
(k≠0)的图象的另一支交于点C,过点B作直线l垂直于x轴,点E是点D关于直线l的对称点.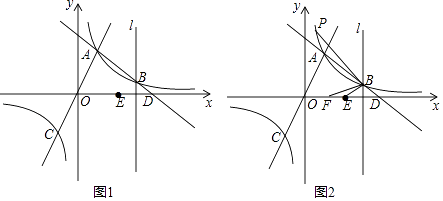
(1)k=;
(2)判断点B,E,C是否在同一条直线上,并说明理由;
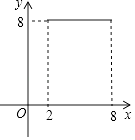
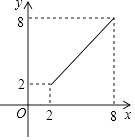
(3)如图2,已知点F在x轴正半轴上,OF= ![]() ,点P是反比例函数y=
,点P是反比例函数y= ![]() (k≠0)的图象位于第一象限部分上的点(点P在点A的上方),∠ABP=∠EBF,则点P的坐标为( , ).
(k≠0)的图象位于第一象限部分上的点(点P在点A的上方),∠ABP=∠EBF,则点P的坐标为( , ).
【答案】
(1)3
(2)解:点B、E、C在同一条直线上.理由如下:
∵直线OA与反比例函数y= ![]() (k≠0)的图象的另一支交于点C,
(k≠0)的图象的另一支交于点C,
∴点A与点C关于原点对称,
∴C(﹣1,﹣3),
∵B(m,1)在反比例函数y= ![]() 的图象上,
的图象上,
∴1×m=3,解得m=3,即B(3,1),
把A(1,3)代入y=﹣x+b得﹣1+b=3,解得b=4,
∴直线AB的解析式为y=﹣x+4,
当y=0时,﹣x+4=0,解得x=4,则D(4,0),
∵点E与点D关于直线x=3对称,
∴E(2,0),
设直线BC的解析式为y=px+q,
把B(3,1),C(﹣1,﹣3)代入得 ![]() ,解得
,解得 ![]() ,
,
∴直线BC的解析式为y=x﹣2,
当x=2时,y=x﹣2=0,
∴点E在直线BC上,
即点B、E、C在同一条直线上;
(3)![]() ,
,![]()
【解析】解:(1)∵A(1,3)在反比例函数y= ![]() 的图象上,
的图象上, 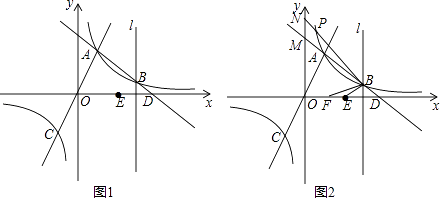
∴k=1×3=3;(3)直线AB交y轴于M,直线BP交y轴于N,如图2,
当x=0时,y=﹣x+4=4,则M(0,4),
而B(3,1),E(2,0),F( ![]() ,0),
,0),
∴BM= ![]() =3
=3 ![]() ,BE=
,BE= ![]() =
= ![]() ,EF=2﹣
,EF=2﹣ ![]() =
= ![]() ,
,
∵OM=OD=4,
∴△OMD为等腰直角三角形,
∴∠OMD=∠ODM=45°,
∵点E与点D关于直线x=3对称,
∴∠BED=∠BDE=45°,
∴∠BMN=∠BEF=135°,
∵∠ABP=∠EBF,
∴△BMN∽△BEF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得MN=
,解得MN= ![]() ,
,
∴N(0, ![]() ),
),
设直线BN的解析式为y=ax+n,
把B(3,1),N(0, ![]() )代入得
)代入得 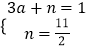 ,解得
,解得 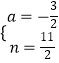 ,
,
∴直线BN的解析式为y=﹣ ![]() x+
x+ ![]() ,
,
解方程组 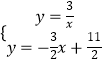 得
得 ![]() 或
或 ![]() ,
,
∴P点坐标为( ![]() ,
, ![]() ).
).
所以答案是3, ![]() ,
, ![]() .
.

【题目】某校九年级两个班,各选派10名学生参加学校举行的“数学奥林匹克”大赛预赛,各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | 94 | b | 93 | 12 |
九(2)班 | 99 | a | 95.5 | 93 | 8.4 |
(1)直接写出表中a、b的值:a= , b=;
(2)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.